揭秘:1度与弧度之间的神秘换算关系
在数学中,角度和弧度是衡量平面角大小的两种基本单位。虽然我们在日常生活中经常使用度数(°)来表示角度,但在许多科学计算和数学分析中,弧度(rad)却更为常用。了解“1度等于多少弧度”这一基本转换关系,对于深入理解三角函数、微积分等领域至关重要。本文旨在清晰、简洁地阐述这一转换关系,同时探讨其背后的数学原理及应用。

首先,明确角度和弧度的定义是理解它们之间转换关系的基础。度数是我们最为熟悉的角度单位,一个完整的圆被划分为360度。而弧度则是基于圆的半径定义的,一个圆的周长与半径之比即为2π(π约等于3.14159),这个比值被定义为360度角对应的弧度值,也即一个完整的圆周角等于2π弧度。

接下来,我们直接解答核心问题:“1度等于多少弧度?”这个转换关系的数学表达式为:1° = π/180 rad。这意味着,要将度数转换为弧度,我们只需将度数乘以π/180。反之,若要将弧度转换为度数,则需将弧度值乘以180/π。这一转换公式的推导源自上述关于角度和弧度定义的对比:一个圆的弧度数为2π,而对应的度数为360°,因此每度对应的弧度即为2π/360,化简得π/180。
理解了这一转换关系后,我们进一步探讨其在实际应用中的重要性。在三角函数领域,弧度制的使用使得函数的周期性和对称性表现得更加直观和简洁。例如,正弦函数sin(x)和余弦函数cos(x)的周期在弧度制下为2π,这一周期性在解决周期性问题时极为方便。此外,弧度制还简化了微积分中对三角函数的求导和积分运算,使得这些运算过程更加直观和易于理解。
在物理学和工程学领域,弧度制同样发挥着重要作用。例如,在力学中,角速度和角加速度通常以弧度/秒(rad/s)为单位,这种表示方法有助于精确描述旋转物体的运动状态。在电气工程中,交流电的相位角也常用弧度表示,这有助于分析和计算电路中的相位关系和功率因数。
此外,弧度制在计算机科学和编程中也有着广泛应用。在图形处理和计算机图形学中,使用弧度制来表示角度可以简化旋转、缩放和变换等操作的计算过程。在数值计算和仿真中,弧度制也有助于提高计算的精度和效率。
值得一提的是,尽管弧度制在许多领域具有显著优势,但度数制在日常生活和某些特定领域(如地理、天文学)中仍然具有不可替代的地位。这主要是因为度数制更易于直观理解和表达,且与人类长期的认知习惯相符。因此,在实际应用中,我们需要根据具体情境和需求选择合适的角度单位。
在结束本文之前,我们通过一个简单的实例来演示度数与弧度之间的转换过程。假设我们有一个45°的角,想要知道它对应的弧度值是多少。根据转换公式,我们只需将45乘以π/180,得到的结果约为0.7854(即π/4)。反之,如果我们有一个弧度值为π/3的角,想要知道它对应的度数是多少,我们只需将π/3乘以180/π,得到的结果为60°。
综上所述,“1度等于多少弧度”这一基本转换关系不仅是数学学习中的基础知识,也是连接不同学科领域、解决实际问题的重要桥梁。通过深入理解这一转换关系及其背后的数学原理,我们可以更好地掌握和应用相关知识,为解决实际问题提供更加准确和高效的工具和方法。同时,我们也应认识到度数制和弧度制各有其优缺点和适用范围,在实际应用中应根据具体需求灵活选择和使用。
- 上一篇: 揭秘歇后语“倒打一耙”的趣味前身
- 下一篇: 揭秘:北京督察局的真实职责是什么?
-
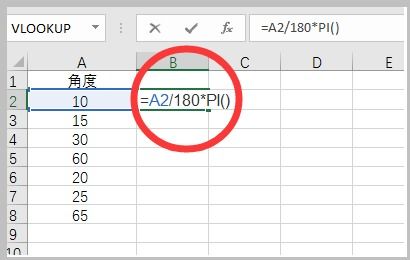 如何将弧度转换为角度?资讯攻略11-09
如何将弧度转换为角度?资讯攻略11-09 -
 揭秘:前度与前任,两者究竟有何不同?资讯攻略01-05
揭秘:前度与前任,两者究竟有何不同?资讯攻略01-05 -
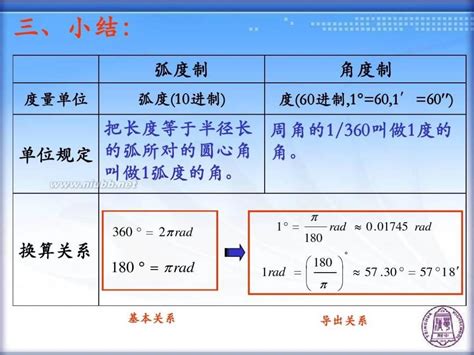 轻松掌握:弧度与角度的换算方法资讯攻略11-15
轻松掌握:弧度与角度的换算方法资讯攻略11-15 -
 揭秘单位换算:如何将1升精准转换为吨?资讯攻略11-17
揭秘单位换算:如何将1升精准转换为吨?资讯攻略11-17 -
 微克与毫克:揭秘它们之间的神奇换算公式!资讯攻略12-07
微克与毫克:揭秘它们之间的神奇换算公式!资讯攻略12-07 -
 揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03
揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03