揭秘:标准差(Standard Deviation)究竟意味着什么?
Standard Deviation:一种衡量数据变异的数值指标

在统计学、数学以及众多科学领域中,标准差(Standard Deviation)是一个非常重要的概念。它为我们提供了一种量化数据变异程度的方法,能够帮助我们更好地理解数据的分布特性。本文将详细介绍标准差的概念、计算方法、应用及其在不同学科中的含义。
标准差(Standard Deviation),英文全称为“Standard Deviation”,简写为SD或σ(sigma)。其定义为真误差平方和的平均数的平方根,是一种在一定条件下衡量测量精度或数据离散程度的数值指标。标准差反映了数据与其平均值(均值)之间的偏差程度,具体表现为数据点围绕均值的分布情况。当数据的标准差较小时,表示数据点相对集中,离散程度较小;而当标准差较大时,表示数据点相对分散,离散程度较大。
从数学角度来看,标准差是方差的平方根。方差(Variance)是每个数据点与均值之差的平方的平均值,它衡量了数据的离散程度,但单位与数据本身的单位不一致。而标准差保留了数据的原始单位,使得其在实际应用中更为直观和方便。
标准差的计算公式如下:
σ=√(∑(x-μ)^2/N)
其中,σ表示标准差,x为各个数据点,μ为均值,N为数据点的数量。通过计算每个数据点与均值的差的平方,然后求这些平方值的平均数,最后取平方根,即可得到标准差。
标准差的应用十分广泛。在数据分析中,它常用于描述数据的离散程度,评估数据的稳定性和可靠性。例如,在市场调研中,可以通过计算消费者对某一产品满意度的标准差,来评估消费者对该产品满意度的离散程度,从而帮助企业了解消费者对产品的整体评价和个体差异。在金融领域,标准差被用于衡量投资组合的风险,通过计算投资组合收益率的标准差,可以评估投资组合的波动性和潜在风险。
此外,标准差在统计学中还经常与其他统计量一起使用,如均值、中位数和众数等。这些统计量共同构成了描述数据集特征的基本框架。例如,均值和标准差结合起来,可以为我们提供一个数据集的中心位置和离散程度的全面描述。
标准差在不同学科中还有其特定的含义和应用。在测绘学中,标准差是真误差平方和的平均数的平方根,用于衡量测量精度和观测值的离散情况。在大气科学中,标准差同样用于评估大气探测数据的精度和离散程度,为气象预报和气候研究提供重要依据。在遗传学领域,标准差作为方差的平方根,表示一组遗传数据的变异程度,为遗传育种和基因研究提供重要参数。
值得注意的是,虽然标准差是一个非常有用的统计量,但在实际应用中也需要注意其局限性。例如,标准差对于极端值的敏感性较高,如果数据集中存在极端值,那么标准差可能会受到较大影响,从而无法准确反映数据的整体离散程度。此外,标准差只能描述数据的离散程度,而不能反映数据的分布形态,如数据的偏态和峰态等。因此,在实际应用中,我们需要结合其他统计量和图形工具,如直方图、箱形图等,来全面描述数据的特征。
除了基本标准差外,还有一些衍生概念,如样本标准差和总体标准差。样本标准差是根据样本数据计算得到的标准差,用于估计总体标准差。总体标准差则是根据全部数据计算得到的标准差,反映了总体数据的离散程度。在实际应用中,我们通常使用样本标准差来估计总体标准差,因为在实际研究中往往难以获取全部数据。
此外,标准差还与一些其他统计概念密切相关,如标准误差(Standard Error)和置信区间(Confidence Interval)。标准误差是样本均值的标准差,用于衡量样本均值与总体均值之间的偏差程度。置信区间则是根据样本数据计算得到的总体均值的可能范围,用于评估样本均值对总体均值的估计精度。这些概念共同构成了统计学中的基本框架,为我们提供了描述和推断总体特征的重要工具。
在经济学和金融学中,标准差通常被称为标准离差,用于衡量投资组合或单一资产的波动性。投资组合的标准差越大,表示其收益率的波动性越大,风险也越高。因此,在投资组合管理中,标准差是一个非常重要的风险指标,可以帮助投资者评估投资组合的风险水平并制定相应的风险管理策略。
在质量控制和工程领域,标准差也被广泛应用。例如,在制造过程中,可以通过计算产品质量的标准差来评估生产过程的稳定性和可控性。如果标准差较小,表示产品质量相对稳定,生产过程可控性较高;而如果标准差较大,则表示产品质量波动较大,生产过程可能存在一些问题或不稳定因素。
此外,标准差还在医学研究中发挥着重要作用。例如,在临床试验中,可以通过计算患者某项生理指标的标准差来评估该指标的离散程度和个体差异。这有助于研究人员了解患者对该指标的响应情况和个体差异,从而为制定更精确的治疗方案和评估疗效提供依据。
综上所述,标准差是一种重要的统计量,用于衡量数据的离散程度和变异程度。它在数据分析、统计学、经济学、金融学、质量控制和医学研究等多个领域中发挥着重要作用。通过计算标准差,我们可以更好地了解数据的分布特征、评估数据的稳定性和可靠性,并为决策和分析提供重要依据。因此,掌握标准差的概念和应用方法对于提高我们的数据分析能力和科学素养具有重要意义。
- 上一篇: QQ观看直播的方法与步骤
- 下一篇: 重启人生:全面掌握‘Life Restart’游戏攻略
-
 Excel中快速计算标准差的简易教程资讯攻略10-25
Excel中快速计算标准差的简易教程资讯攻略10-25 -
 Excel中标准偏差的计算公式资讯攻略11-03
Excel中标准偏差的计算公式资讯攻略11-03 -
 A4纸尺寸与64开纸张对比:究竟差多少?资讯攻略03-03
A4纸尺寸与64开纸张对比:究竟差多少?资讯攻略03-03 -
 如何在Excel中计算标准差?资讯攻略11-03
如何在Excel中计算标准差?资讯攻略11-03 -
 想知道Excel中如何轻松计算标准差?一招搞定,点击进来学!资讯攻略10-25
想知道Excel中如何轻松计算标准差?一招搞定,点击进来学!资讯攻略10-25 -
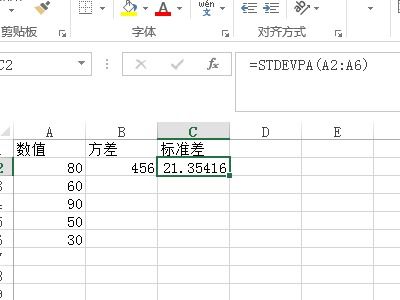 Excel轻松计算标准差教程资讯攻略10-27
Excel轻松计算标准差教程资讯攻略10-27











