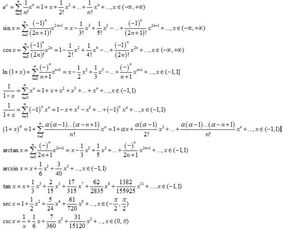频率的计算公式是什么
在物理学和工程学中,频率公式是理解和分析周期性现象的重要工具。频率描述了单位时间内某一事件重复发生的次数,通常以赫兹(Hz)为单位,即每秒钟发生的次数。通过频率公式,我们可以从多个维度深入了解周期性信号的特性和行为。
频率公式的基本定义

f = 1/T

这个公式告诉我们,频率与周期成反比:周期越长,频率越低;周期越短,频率越高。频率是描述周期性振动、波动或信号特性的关键参数,无论是声波、电磁波还是机械振动,频率都是其核心属性之一。

从物理振动的角度看频率公式
在物理学中,频率公式常常用于描述简谐振动。简谐振动是指物体围绕其平衡位置进行周期性、往复性的运动,如弹簧振子的振动或单摆的摆动。在简谐振动中,频率与系统的固有属性密切相关。
对于弹簧振子,其频率公式为:
f = (1/(2π)) * √(k/m)
其中,k是弹簧的劲度系数,m是振子的质量。这个公式表明,弹簧振子的频率与弹簧的劲度系数成正比,与振子的质量成反比。
对于单摆,其频率公式为:
f = (1/(2π)) * √(g/L)
其中,g是重力加速度,L是摆长。这个公式说明,单摆的频率与重力加速度的平方根成正比,与摆长的平方根成反比。
从声波的角度看频率公式
在声学领域,频率公式用于描述声波的特性。声波是机械波的一种,通过介质(如空气、水等)中的分子振动传播。声波的频率决定了我们听到的音调的高低。
对于声波,频率公式仍然是f = 1/T,但这里的周期T指的是声波中某一特定点(如压力最大点或位移最大点)从一次最大值回到下一次最大值所需的时间。声波的频率范围非常广泛,从人类能听到的20Hz到20kHz,到超声波的几十kHz以上,甚至到次声波的几Hz以下。
从电磁波的角度看频率公式
在电磁学中,频率公式同样具有重要地位。电磁波是由变化的电场和磁场交替产生并传播的波动现象,包括无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线等。电磁波的频率决定了其能量大小和穿透能力。
对于电磁波,频率公式同样是f = 1/T,但这里的周期T指的是电磁波中电场或磁场从最大值到下一个最大值所需的时间。电磁波的频率与波长(λ)和波速(c)之间还有另一个重要关系,即:
c = λf
这个公式是电磁波的基本性质之一,表明电磁波在真空中的传播速度(光速)是恒定的,而波长和频率成反比。不同频率的电磁波具有不同的物理特性和应用,如无线电通信、雷达探测、光谱分析等。
从信号处理的角度看频率公式
在信号处理领域,频率公式用于分析信号的频谱特性。信号可以看作是时间和幅度(或相位)的函数,而频谱则是信号在频率域上的表示。通过分析信号的频谱,我们可以了解信号的频率成分、带宽、能量分布等信息。
在数字信号处理中,常用的频率分析工具是傅里叶变换。傅里叶变换将时域信号转换为频域信号,从而可以直观地看到信号的频率成分。对于离散时间信号x[n],其离散傅里叶变换(DFT)的公式为:
X[k] = Σ x[n] * exp(-j2πkn/N) (n=0,1,...,N-1)
其中,X[k]是信号x[n]在频域上的表示,N是信号的长度,j是虚数单位。虽然这个公式看起来比简单的频率公式复杂得多,但它实际上是频率分析在数字信号处理中的具体应用。
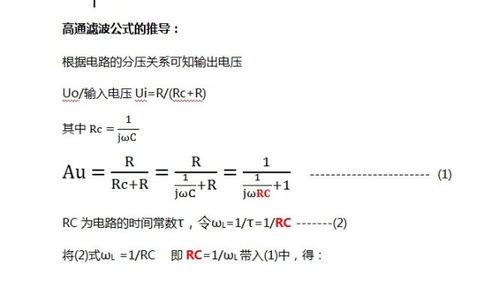
从工程应用的角度看频率公式
在工程实践中,频率公式广泛应用于各种领域。例如,在机械工程中,频率公式用于设计和分析振动系统,如减震器、滤波器等。在电子工程中,频率公式用于设计和调试电路,如振荡器、滤波器等。在通信工程中,频率公式用于设计和优化通信系统,如调制器、解调器、频率合成器等。
此外,频率公式还在生物医学、天文学、地球物理学等领域发挥着重要作用。例如,在生物医学中,心电图(ECG)和脑电图(EEG)等生物电信号的频率分析有助于诊断心脏疾病和神经系统疾病。在天文学中,恒星的振动频率(即星震学)有助于了解恒星的内部结构和演化过程。在地球物理学中,地震波的频率分析有助于确定地震的震源位置、震级和地震波的传播特性。
总结
频率公式是描述周期性现象的重要工具,它揭示了频率与周期、波长、波速等物理量之间的关系。从物理振动的角度看,频率公式描述了简谐振动的固有属性;从声波和电磁波的角度看,频率公式揭示了声音和光的传播特性;从信号处理的角度看,频率公式用于分析信号的频谱特性;从工程应用的角度看,频率公式广泛应用于各种领域,为工程设计和优化提供了有力支持。
通过学习和掌握频率公式,我们可以更深入地理解周期性现象的本质和规律,为科学研究和技术创新提供坚实的理论基础。同时,频率公式也提醒我们,在分析和解决实际问题时,要充分考虑周期性因素的影响,以确保结果的准确性和可靠性。
- 上一篇: 一键直达!快速显示桌面的绝妙技巧
- 下一篇: 淘宝客服介入,一键直达指南!
-
 三相电功率计算公式详解资讯攻略10-28
三相电功率计算公式详解资讯攻略10-28 -
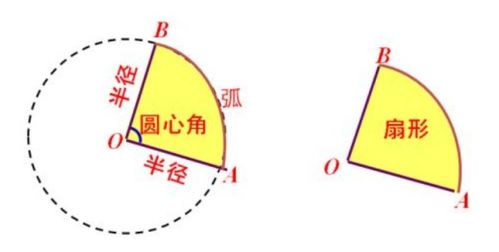 扇形面积计算的三大公式是什么?资讯攻略10-25
扇形面积计算的三大公式是什么?资讯攻略10-25 -
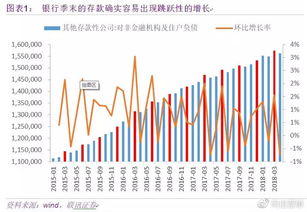 资深解析:银行存款偏离度计算公式是什么?怎么运用?资讯攻略12-05
资深解析:银行存款偏离度计算公式是什么?怎么运用?资讯攻略12-05 -
 电离度的计算公式是什么?资讯攻略11-01
电离度的计算公式是什么?资讯攻略11-01 -
 水厂配水电耗定义及计算公式是什么(单位:Kwh)?资讯攻略12-06
水厂配水电耗定义及计算公式是什么(单位:Kwh)?资讯攻略12-06 -
 工程力学中惯性矩的定义和计算公式是什么?资讯攻略02-13
工程力学中惯性矩的定义和计算公式是什么?资讯攻略02-13