揭秘：惯性矩的精准计算公式大公开！

惯性矩计算公式详解

在力学领域中，惯性矩是一个至关重要的概念，它描述了截面抵抗弯曲的性质。惯性矩（也称为转动惯量或矩量惯性）是物体相对于某一旋转点（或轴）的质量分布的一种度量。了解惯性矩的计算公式及其在不同几何形状中的应用，对工程师、物理学家以及其他相关专业人员至关重要。本文将详细介绍惯性矩的计算公式，并探讨其在几种常见几何形状中的应用，力求内容简洁明了，提高用户阅读体验和搜索引擎友好度。

惯性矩的基本概念

惯性矩是描述物体在旋转运动中惯性大小的物理量。具体来说，它是指物体在受到外力矩作用时，产生角加速度的难易程度。惯性矩的大小与物体的质量分布以及旋转轴的位置密切相关。惯性矩的公式可以表示为：

\[ I = \sum (m_i r_i^2) \]

其中，\(I\) 表示惯性矩，\(m_i\) 表示物体中第 \(i\) 个质点的质量，\(r_i\) 表示该质点到旋转轴的距离。

常见几何形状的惯性矩计算公式

不同形状的物体具有不同的惯性矩计算公式。以下是几种常见几何形状（矩形、三角形、圆形和环形）的惯性矩计算公式。

矩形

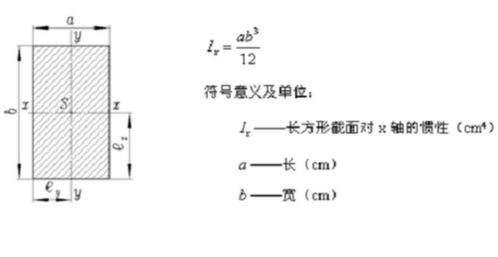
对于矩形截面，其惯性矩计算公式为：

\[ I = \frac{b \cdot h^3}{12} \]

其中，\(b\) 表示矩形的宽度，\(h\) 表示矩形的高度。这个公式假设矩形绕其高度方向（垂直于底边的方向）旋转。

三角形

对于等边三角形截面，其惯性矩计算公式为：

\[ I = \frac{b \cdot h^3}{36} \]

同样，\(b\) 表示三角形的底边长度，\(h\) 表示三角形的高度。这个公式假设三角形绕其高度方向（垂直于底边的方向）旋转。

圆形

对于圆形截面，其惯性矩计算公式为：

\[ I = \frac{\pi \cdot d^4}{64} \]

或者：

\[ I = \frac{\pi \cdot r^4}{4} \]

其中，\(d\) 表示圆的直径，\(r\) 表示圆的半径。这个公式假设圆绕其直径方向（或圆心）旋转。

环形

对于环形截面（也称为空心圆），其惯性矩计算公式为：

\[ I = \frac{\pi \cdot D^4 \cdot (1 - \alpha^4)}{64} \]

其中，\(D\) 表示环形的外径，\(\alpha\) 表示环形的内径与外径之比（即 \(\alpha = \frac{d}{D}\)），\(d\) 表示环形的内径。这个公式假设环形绕其圆心旋转。

惯性矩的应用

惯性矩在工程和物理学中具有广泛的应用。以下是一些具体的应用场景：

1. 结构力学：在结构设计中，惯性矩用于计算梁的弯曲应力。较大的惯性矩可以提高梁的抗弯能力，从而提高结构的整体稳定性。

2. 动力学：在刚体动力学中，惯性矩用于描述刚体绕某轴的转动惯量。它是分析刚体转动运动的基础。

3. 机械振动：在机械振动分析中，惯性矩用于计算系统的固有频率和模态。这对于设计减振系统和控制振动非常有用。

4. 航空航天：在航空航天工程中，惯性矩用于计算飞行器的姿态控制和稳定性。正确的惯性矩计算有助于确保飞行器的安全飞行。

实例分析

为了更好地理解惯性矩的概念和计算方法，以下通过一个简单的实例进行分析。

假设有一个矩形截面梁，其宽度 \(b = 0.2\) 米，高度 \(h = 0.4\) 米。我们需要计算该梁绕其高度方向的惯性矩。

根据矩形截面惯性矩的计算公式：

\[ I = \frac{b \cdot h^3}{12} \]

将 \(b\) 和 \(h\) 的值代入公式中：

\[ I = \frac{0.2 \cdot 0.4^3}{12} = \frac{0.2 \cdot 0.064}{12} = 0.001067 \text{ m}^4 \]

因此，该矩形截面梁绕其高度方向的惯性矩为 \(0.001067\) 平方米四次方。

注意事项

在计算惯性矩时，需要注意以下几点：

1. 选择合适的旋转轴：惯性矩是相对于某一旋转轴而言的。在计算时，必须明确旋转轴的位置和方向。

2. 考虑质量分布：惯性矩与物体的质量分布密切相关。在计算时，必须准确知道物体的质量分布情况。

3. 选择合适的公式：不同形状的物体具有不同的惯性矩计算公式。在计算时，必须选择正确的公式。

4. 单位一致性：在计算惯性矩时，必须确保所有物理量的单位一致。例如，长度单位可以是米（m），质量单位可以是千克（kg），那么惯性矩的单位就是平方米四次方（m^4）。

结语

惯性矩是描述物体抵抗弯曲性质的物理量，在力学和工程领域具有广泛的应用。通过了解不同几何形状的惯性矩计算公式，我们可以更好地分析物体的转动运动和弯曲应力。本文详细介绍了惯性矩的基本概念、常见几何形状的惯性矩计算公式以及其在工程和物理学中的应用。希望这些内容能够帮助读者更好地理解和掌握惯性矩的相关知识。

在未来的学习和工作中，我们应该继续深入研究惯性矩的性质和应用，不断探索新的计算方法和应用场景。同时，我们也应该注重实践经验的积累，通过实际操作和案例分析来提高自己的专业技能和实践能力。只有这样，我们才能更好地应对复杂多变的工程问题，为社会的发展和进步做出更大的贡献。