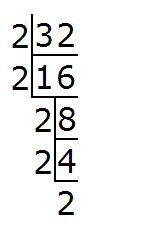揭秘质因数的神奇世界
质因数是什么?

在数学的世界里,质因数是一个既基础又充满魅力的概念。当我们尝试理解一个数的构成时,质因数就像是一把钥匙,帮助我们揭开数字背后的秘密。那么,质因数到底是什么呢?让我们一起深入探讨。

质因数,首先涉及两个关键概念:质数和因数。质数,是一个大于1的自然数,它只有两个正因数:1和它本身。例如,2、3、5、7、11等都是质数。而因数,则是能够整除给定数的数。比如,6的因数有1、2、3和6。现在,将这两个概念结合起来,质因数就是一个数的因数,并且这个因数还是质数。
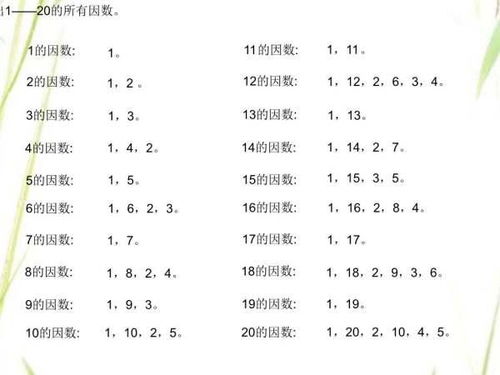
举个例子,数字12可以被分解为1×12、2×6、3×4等几种因数组合。但如果我们进一步观察,会发现其中只有2和3是质数,而1、12、6、4都不是(1不是质数也不是合数,但在此讨论质因数时,我们主要关注大于1的质数)。因此,12的质因数是2和3。这意味着,12可以表示为2的2次方与3的1次方的乘积,即12=2²×3。
质因数的概念在数学的多个领域中都发挥着重要作用。首先,在数论中,质因数是研究整数性质的基础。通过对一个数进行质因数分解,我们可以更深入地了解这个数的构成和性质。例如,判断一个数是否为质数,一个简单的方法就是看它是否只能被1和自身整除(当然,对于较大的数,这种方法效率较低,通常会采用其他算法)。此外,质因数分解还可以帮助我们求解一些与整数相关的数学问题,如求最大公约数(GCD)和最小公倍数(LCM)等。
在代数中,质因数分解也是解决方程和不等式的重要手段。例如,在解一元二次方程ax²+bx+c=0时,如果我们知道a、b、c的质因数分解形式,就可以更容易地找到方程的根。此外,在解决一些涉及分数的问题时,通过质因数分解,我们可以更清晰地看到分子和分母之间的关系,从而更容易地进行约分和通分。
质因数分解在几何和组合数学中也有广泛的应用。例如,在几何中,我们可以利用质因数分解来求解一些与面积和体积相关的问题。在组合数学中,质因数分解可以帮助我们计算一些排列、组合和概率问题的结果。
除了在数学领域的应用外,质因数在现实生活中也有着广泛的用途。在计算机科学中,质因数分解是许多加密算法的基础。例如,在RSA加密算法中,公钥和私钥的生成都依赖于大整数的质因数分解。由于质因数分解的复杂性随着数的增大而急剧增加,因此目前还没有一种高效的算法能够快速地分解大整数。这使得RSA加密算法在信息安全领域得到了广泛的应用。
在金融领域,质因数分解也有着重要的应用。例如,在风险评估中,我们可以利用质因数分解来识别和分析影响风险的各种因素。通过对这些因素进行量化和分析,我们可以更准确地评估风险的大小和可能性,从而制定更有效的风险管理策略。
此外,质因数分解还在物理学、化学、生物学等其他学科中发挥着重要作用。例如,在物理学中,质因数分解可以帮助我们理解和计算一些与量子数和能级相关的问题。在化学中,质因数分解可以用于分析化合物的组成和性质。在生物学中,质因数分解可以用于研究生物体的遗传信息和基因表达等。
那么,如何找到一个数的质因数呢?最常用的方法是试除法。我们从最小的质数2开始,逐一尝试去除这个数,直到除尽或者无法再除为止。如果能整除,那么这个质数就是这个数的一个质因数;如果不能整除,我们就尝试下一个质数。例如,要找到28的质因数,我们可以从2开始试除:28÷2=14(能整除,2是质因数),然后14÷2=7(能整除,2也是质因数),最后7无法再被2整除,但7本身是质数,所以也是质因数。因此,28的质因数是2和7(或表示为2²×7)。
当然,对于较大的数,试除法可能效率较低。这时,我们可以采用一些更高效的算法,如筛法(如埃拉托斯特尼筛法)和分解算法(如Pollard的ρ算法、二次筛法等)。这些算法可以在更短的时间内找到一个数的质因数分解形式。
值得一提的是,质因数分解在数学界还有一个著名的未解之谜——哥德巴赫猜想。这个猜想提出:任何大于2的偶数都可以表示为两个质数之和。虽然数学家们已经证明了许多与哥德巴赫猜想相关的命题,但至今仍未找到这个猜想的完整证明。这也使得质因数分解在数学界保持着持久的魅力和神秘感。
质因数不仅是数学中的一个基础概念,更是连接数学与现实世界的桥梁。通过质因数分解,我们可以更深入地理解数字的本质和性质,也可以将数学知识应用到其他领域中去解决实际问题。因此,掌握质因数的概念和性质对于我们来说是非常重要的。
总之,质因数是一个既简单又深刻的数学概念。它既是数学研究的基础工具之一,也是连接数学与现实世界的纽带。通过深入学习和理解质因数的性质和应用,我们可以更好地掌握数学知识并运用到实际生活中去。希望这篇文章能够帮助你更好地了解质因数并激发你对数学的兴趣和热爱!
- 上一篇: 揭秘:女孩子发77777背后的神秘梗意!
- 下一篇: 解析:'欧尼酱'的含义是什么
-
 质因数是如何定义的?资讯攻略02-11
质因数是如何定义的?资讯攻略02-11 -
 揭秘:30的所有因数是什么?资讯攻略03-06
揭秘:30的所有因数是什么?资讯攻略03-06 -
 功率因数计算公式的求解方法资讯攻略10-31
功率因数计算公式的求解方法资讯攻略10-31 -
 揭秘:数字5360背后的神秘含义是什么?资讯攻略12-06
揭秘:数字5360背后的神秘含义是什么?资讯攻略12-06 -
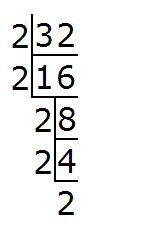 32的因数包括哪些?资讯攻略01-10
32的因数包括哪些?资讯攻略01-10 -
 掌握网上国网查询技巧:轻松了解功率因数调整电费详情资讯攻略11-04
掌握网上国网查询技巧:轻松了解功率因数调整电费详情资讯攻略11-04