三次对折后绳子刚好达井底,井深四米,绳子原长多少米?
在探讨一个看似简单却蕴含深刻数学原理的问题——“一口井深4米,把一根绳子对折三次,绳子长多少米?”时,我们不禁要深入到这个问题的本质,理解对折的含义,以及它如何与绳子的长度和井的深度相关联。这个问题不仅考验了我们的数学逻辑,还激发了对日常生活中数学现象的好奇心和探索欲。

首先,让我们明确问题中的关键信息:井的深度是4米,绳子被对折了三次。对折,这个动作,在数学和物理学中都是一个重要的概念,它涉及到长度的减半、面积的四分之一、体积的八分之一等比例关系。当我们说一根绳子对折一次时,它的长度就变成了原来的一半;对折两次,长度变为四分之一;对折三次,则是八分之一。这个规律是基于几何级数的减少,每一次对折都会使绳子的长度以2的幂次方减少。
现在,让我们将这个规律应用到具体的问题中。假设绳子的原始长度为L米。当绳子对折一次后,其长度变为L/2米;对折两次,长度变为L/4米;对折三次,长度则是L/8米。这里的关键在于,我们需要找到一个合适的L值,使得对折三次后的绳子长度能够满足某种条件——在这个问题中,这个条件是绳子对折后的长度至少要比井的深度(4米)长,否则绳子就无法被用来测量井深(当然,题目并未明确要求绳子必须完全放入井中,但这是我们解决问题的逻辑起点)。
然而,如果我们仅仅根据对折后的长度(L/8)与井深(4米)进行比较,我们会发现这个问题其实缺少了一个直接求解L的足够条件。因为对于任何大于32米的绳子长度L(即L/8>4),对折三次后的长度都会超过井深。这意味着,题目实际上是在询问一个范围,而不是一个具体的值。换句话说,只要绳子的原始长度超过32米,无论它有多长,对折三次后都能满足比井深4米要长的条件。
但是,如果我们进一步分析题目,可能会发现隐藏在其后的另一个层面的问题:如果我们要用最短的绳子来完成这个任务(即对折三次后刚好或稍微超过井深),那么这根绳子的长度应该是多少呢?这里,我们需要找到一个最小的L值,使得L/8略大于或等于4。显然,这个最小的L值是32米(因为32/8=4),但如果你想要绳子对折后稍微超出井口一点(比如为了确保安全或操作方便),你可能需要选择比32米稍长一些的绳子。
不过,这里还有一个有趣的思考方向:如果绳子的长度是有限的,比如我们只有一根16米长的绳子,那么它对折两次后(16/4=4米)就刚好等于井深,但对折三次(16/8=2米)就不足以到达井底了。这种情况下,我们不得不寻找其他方法来解决测量井深的问题,比如使用更长的绳子、其他测量工具或者不同的测量方法。
此外,这个问题还可以引发我们对数学中比例、分数和几何级数等概念的深入思考。比如,我们可以尝试用不同的对折次数来观察绳子长度的变化规律,或者比较不同长度的绳子在对折相同次数后的结果。这些探索不仅能够帮助我们更好地理解数学原理,还能激发我们的创造力和解决问题的能力。
在实际生活中,类似的问题也层出不穷。比如,在装修房屋时,我们需要计算墙壁或地板的面积来购买足够的涂料或地板砖;在制作手工艺品时,我们需要根据材料的尺寸和形状来设计图案和切割方式;在烹饪时,我们需要根据食材的分量和食谱的比例来调配调料和烹饪时间。这些问题都涉及到对长度、面积、体积和比例等数学概念的准确理解和应用。
回到最初的问题上来,虽然我们无法给出一个具体的绳子长度作为答案(除非我们设定一个额外的条件,比如绳子对折后必须刚好到达井底或者超出井口一定距离),但我们可以通过分析这个问题来加深对数学原理的理解和应用能力。同时,这个问题也提醒我们,在日常生活中遇到问题时,要善于运用数学和逻辑思维来寻找解决方案。
最后,值得注意的是,这个问题虽然简单,但它所蕴含的数学原理和思维方式却是我们学习和成长过程中不可或缺的。通过不断地思考和探索,我们不仅能够提高自己的数学水平,还能够培养自己的创新思维和解决问题的能力。因此,让我们在面对问题时保持好奇心和探索欲,勇敢地迎接每一个挑战吧!
- 上一篇: 水落石出,揭秘隐藏的生肖之谜
- 下一篇: 揭秘《等不到花开》原唱之声,探寻歌曲背后的故事
-
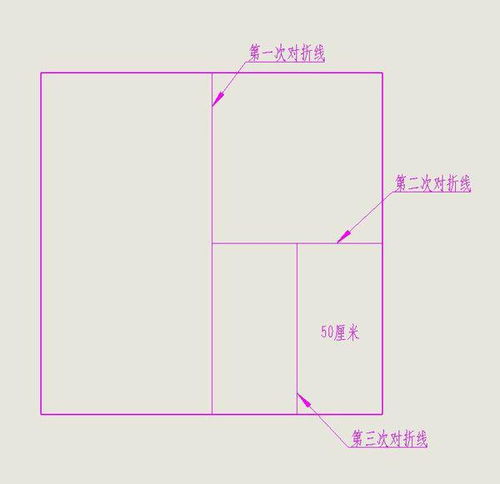 一根绳子对折三次后刚好达到4米深井底,绳子原长多少米?资讯攻略01-28
一根绳子对折三次后刚好达到4米深井底,绳子原长多少米?资讯攻略01-28 -
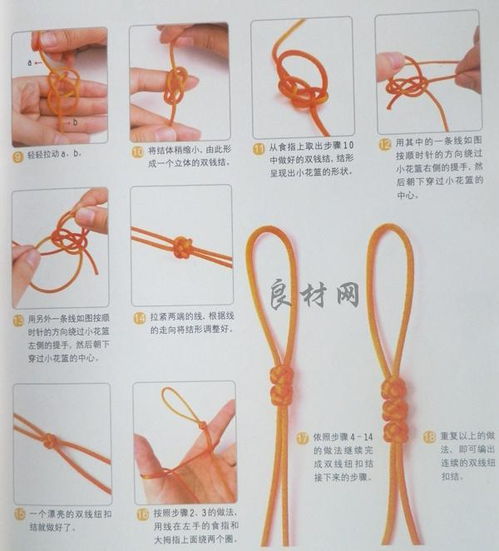 双线头纽扣结编织教程图解资讯攻略11-18
双线头纽扣结编织教程图解资讯攻略11-18 -
 轻松掌握吊坠打结技巧资讯攻略10-31
轻松掌握吊坠打结技巧资讯攻略10-31 -
 轻松学会!挂坠绳子打结技巧大揭秘资讯攻略10-31
轻松学会!挂坠绳子打结技巧大揭秘资讯攻略10-31 -
 吊坠如何正确打结?资讯攻略11-04
吊坠如何正确打结?资讯攻略11-04 -
 玉佩吊坠的简易绑绳教程资讯攻略11-14
玉佩吊坠的简易绑绳教程资讯攻略11-14












