揭秘比的化简:简化比例的艺术
比的化简是数学中一个基础且重要的概念,它涉及到比、分数、小数之间的转换以及简化。在学习比的化简之前,我们需要先理解什么是比。比通常用来表示两个数量之间的关系,它告诉我们一个数量是另一个数量的多少倍。比如,如果说“5比3”,这就意味着5是3的约1.67倍(这里的1.67是一个近似值,实际上是一个无限循环小数)。

在数学中,比的化简就是将一个比转换成最简形式的过程。所谓最简形式,就是比的前项和后项没有其他公约数(除了1)的比。化简比的过程,实际上就是寻找这两个数的最大公约数,并用它们分别去除这两个数,从而得到最简比。

为了深入理解比的化简,我们可以从以下几个方面来探讨:
一、比的基本概念
比由两个数相除表示,一般写成“a:b”或“a/b”的形式,其中a是比的前项,b是比的后项。比如,“4:6”或“4/6”就是一个比。在实际应用中,比常常用来表示两个量之间的相对关系,比如速度(距离与时间的比)、效率(产出与投入的比)等。
二、比的化简方法
1. 找最大公约数:化简比的第一步是找到比的前项和后项的最大公约数。最大公约数是两个或多个整数共有约数中最大的一个。例如,对于比“12:18”,我们可以发现12和18的最大公约数是6。
2. 分别除以最大公约数:找到最大公约数后,我们将比的前项和后项分别除以这个最大公约数。这样,我们就可以得到一个最简形式的比。继续上面的例子,“12:18”化简后就是“2:3”。
3. 特殊情况的化简:有些比可能包含小数或分数。在这种情况下,我们可能需要先将它们转换成整数比,然后再进行化简。例如,比“0.5:0.25”可以先转换成“5:2.5”(这里我们乘以了10来消除小数),然后再化简成“2:1”。
三、比的化简与分数、小数的关系
比、分数和小数在数学中是紧密相连的。了解它们之间的关系可以帮助我们更好地理解和化简比。
1. 比与分数:比“a:b”可以写成分数“a/b”的形式。因此,化简比的过程实际上就是化简分数的过程。当我们化简一个分数时,我们寻找分子和分母的最大公约数,并用它去除这两个数,从而得到一个最简分数。
2. 比与小数:有时,比可能以小数的形式出现。在这种情况下,我们可以先将小数转换成分数,然后再进行化简。例如,比“0.75:0.25”可以转换成“3/4:1/4”,然后再化简成“3:1”。
四、比的化简在实际问题中的应用
比的化简不仅是一个纯粹的数学问题,它在实际生活中也有广泛的应用。
1. 比例尺:在地图制作中,比例尺是用来表示地图上的距离与实际距离之间的比。化简比例尺可以帮助我们更准确地理解地图上的信息。例如,一个比例尺可能是“1:50000”,这意味着地图上1单位的距离代表实际上的50000单位的距离。
2. 烹饪:在烹饪中,我们经常需要按照一定比例混合各种食材。化简这些比例可以帮助我们更精确地计量食材,从而制作出美味的菜肴。例如,一个食谱可能要求我们用“3杯面粉:2杯水”的比例来制作面团。化简后,这个比例就是“3:2”,这样我们就可以更容易地按照这个比例来计量食材。
3. 金融投资:在金融投资中,我们可能需要比较不同投资产品的回报率。化简这些回报率可以帮助我们更直观地了解哪个产品更有价值。例如,如果我们有两个投资产品,它们的年回报率分别是“8%”和“12%”,那么我们可以直接比较这两个数字而不需要进行化简。但是,如果它们的年回报率分别是“0.08”和“0.12”(以小数形式表示),那么将它们化简成“8%”和“12%”就更有助于我们进行比较。
五、比的化简的注意事项
在化简比的过程中,我们需要注意以下几点:
1. 保持比的意义不变:化简比的过程中,我们需要确保比的意义保持不变。这意味着我们不能随意改变比的前项和后项的值,而只能通过除以它们的最大公约数来化简比。
2. 注意比的前项和后项的顺序:在数学中,比是有序的。这意味着“a:b”和“b:a”表示的是两个不同的比。因此,在化简比时,我们需要注意保持比的前项和后项的顺序不变。
3. 处理特殊情况的比:有些比可能包含0或负数。对于这样的比,我们需要特别注意化简的方法。例如,比“0:5”无法化简,因为它表示一个不存在的关系(0是任何数的0倍)。同样地,比“-3:4”也不能简单地通过除以它们的最大公约数来化简,因为负号会影响比的意义。
4. 避免误解:有时,我们可能会将化简比与约分混淆。约分是指将一个分数的分子和分母同时除以它们的最大公约数,从而得到一个最简分数。虽然化简比和约分在过程上有些相似(都需要找到最大公约数并进行除法运算),但它们的对象和结果是不同的。化简比的对象是两个数的比,而约分的对象是一个分数;化简比的结果是得到一个最简形式的比,而约分的结果是得到一个最简形式的分数。
总之,比的化简是数学中一个基础且重要的概念。通过理解比的基本概念、掌握化简比的方法以及了解比与分数、小数之间的关系,我们可以更好地理解和应用这个概念。同时,在实际问题中灵活运用比的化简技巧也可以帮助我们更准确地理解和解决问题。
- 上一篇: 揭秘:欲钱买乘龙快婿,对应的生肖究竟是谁?
- 下一篇: 揭秘:口若悬河代表的是哪个生肖?
-
 如何理解位移比?掌握位移比调整的实用方法资讯攻略12-07
如何理解位移比?掌握位移比调整的实用方法资讯攻略12-07 -
 隶书‘福’字书写教程资讯攻略10-27
隶书‘福’字书写教程资讯攻略10-27 -
 揭秘:量比究竟是什么?资讯攻略11-07
揭秘:量比究竟是什么?资讯攻略11-07 -
 学习化妆的成本究竟是多少?资讯攻略11-29
学习化妆的成本究竟是多少?资讯攻略11-29 -
 揭秘电脑黑客的高超技巧,让你大开眼界!资讯攻略03-04
揭秘电脑黑客的高超技巧,让你大开眼界!资讯攻略03-04 -
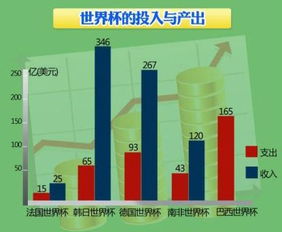 如何计算投入产出比资讯攻略11-16
如何计算投入产出比资讯攻略11-16












