掌握对数收益率的计算与应用技巧
在金融市场的波涛汹涌中,投资者们总是在寻找那把能打开财富之门的钥匙。而在这场智慧的较量中,“对数收益率”这一概念,宛如一盏明灯,指引着人们更加精准地把握市场的脉动。今天,就让我们一同踏上探索之旅,揭开对数收益率的神秘面纱,学习如何理解和计算这一金融分析中的利器。

对数收益率:金融分析的瑞士军刀
想象一下,你是一位航海家,在浩瀚无垠的金融海洋中航行。市场的波动如同海上的风浪,时而平静温柔,时而汹涌澎湃。为了在这片海域中稳健前行,你需要一把能够精确测量风浪强度的“瑞士军刀”——对数收益率。它不仅能够帮助你量化价格的变动,还能揭示价格变动背后的深层规律,为你的投资决策提供坚实的依据。

从百分比收益率说起
在深入探讨对数收益率之前,让我们先回顾一下它的“前辈”——百分比收益率。百分比收益率,简而言之,就是资产价格变动相对于原始价格的百分比。它直观易懂,是许多投资者初步接触市场时首选的分析工具。然而,随着投资经验的积累,人们逐渐发现,百分比收益率在处理连续的价格变动时,可能会因为累积效应而产生偏差,尤其是在价格变动幅度较大或频繁时。

对数收益率:精准量化的新选择
正是在这样的背景下,对数收益率应运而生。与百分比收益率不同,对数收益率通过取自然对数的方式,巧妙地规避了累积效应带来的偏差。它基于数学中的对数变换原理,将价格变动转化为一个连续、可加的度量标准。这一转变,使得对数收益率在衡量资产价格变动时更加精准、稳定,尤其在处理时间序列数据时展现出无可比拟的优势。
对数收益率的魅力所在
那么,对数收益率究竟有何魅力,能够吸引众多投资者和金融分析师的目光呢?
1. 时间加和性:对数收益率的一个重要特性是其时间加和性。这意味着,无论你将观察期划分为多少个时间段,计算得到的对数收益率之和总等于整个观察期的对数收益率。这一特性极大地便利了跨期分析和长期投资规划。
2. 正态分布倾向:金融市场中的许多资产价格变动往往呈现出尖峰厚尾的非正态分布特征。而对数收益率通过对数变换,能够在一定程度上减轻这种非正态性,使得数据更接近正态分布。这对于基于正态分布的统计分析和风险管理至关重要。
3. 复利效应的自然体现:在金融世界中,复利效应无处不在。对数收益率正是复利计算的自然对数形式,因此它能够更准确地反映资产在连续时间内的增值情况。这对于计算复合收益率、评估投资组合表现等方面具有重要意义。
如何计算对数收益率?
既然对数收益率如此神奇,我们何不亲手来尝试一下它的计算方法呢?
步骤一:收集价格数据
首先,你需要收集资产在连续时间点的价格数据。这些数据可以是股票的收盘价、债券的市场价值、商品期货的结算价等。确保数据的时间间隔一致,以便后续计算。
步骤二:计算价格比率
接下来,计算相邻时间点之间的价格比率。对于股票等资产,这通常意味着将后一个时间点的价格除以前一个时间点的价格。这一步骤得到的是价格相对变动的直接度量。
步骤三:应用对数变换
现在,对步骤二中得到的价格比率取自然对数。这一步骤是将对数收益率与百分比收益率区分开的关键所在。通过取对数,你将价格比率的非线性变动转化为线性变动,从而便于后续的分析和计算。
步骤四:整理结果
最后,将每个时间段的对数收益率整理成时间序列数据。这样,你就可以利用这些数据进行进一步的分析和建模了。
对数收益率的应用实例
理论讲解至此,或许你已迫不及待想要看看对数收益率在实际中的应用了。以下是一些典型的应用场景:
1. 风险管理:利用对数收益率计算资产的历史波动率和相关系数,帮助投资者构建风险分散的投资组合。
2. 业绩评估:通过比较不同投资组合的对数收益率,客观评价基金经理的投资能力和策略的有效性。
3. 市场预测:结合时间序列分析和机器学习技术,利用对数收益率预测资产价格的未来走势。
4. 期权定价:在布莱克-舒尔斯期权定价模型中,对数收益率是计算资产未来价格分布的关键参数之一。
结语:对数收益率——金融智慧的结晶
在金融市场的探索之旅中,对数收益率无疑是我们不可或缺的智慧伙伴。它以其独特的数学魅力、精准的量化能力和广泛的应用前景,成为了投资者和金融分析师手中的得力工具。通过深入理解和熟练掌握对数收益率的计算方法及应用技巧,你将能够更加从容地应对市场的风云变幻,捕捉那些稍纵即逝的投资机遇。让我们携手前行,在金融的海洋中扬帆远航,共同追寻那璀璨的财富之光!
- 上一篇: 中国三大岛屿按面积从小到大分别是什么?
- 下一篇: 刘涛一共有几个孩子?
-
 WPS表格高效办公:精通YEARFRAC函数的绝妙技巧资讯攻略11-14
WPS表格高效办公:精通YEARFRAC函数的绝妙技巧资讯攻略11-14 -
 高效数学速算技巧大全资讯攻略11-08
高效数学速算技巧大全资讯攻略11-08 -
 余额宝收益计算方法详解资讯攻略12-04
余额宝收益计算方法详解资讯攻略12-04 -
 余额宝收益计算详解资讯攻略11-03
余额宝收益计算详解资讯攻略11-03 -
 余额宝的利息是如何计算的?资讯攻略11-12
余额宝的利息是如何计算的?资讯攻略11-12 -
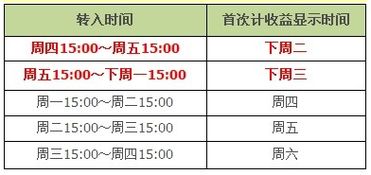 周五转入余额宝,何时开始享收益?资讯攻略11-28
周五转入余额宝,何时开始享收益?资讯攻略11-28












