弧度单位的定义是什么？

在数学和物理学中，弧度是一个至关重要的概念，尤其在处理圆、角度、三角函数以及周期函数时。为了深入探讨这一话题，我们需要明确弧度的单位以及它在各种场合下的应用。

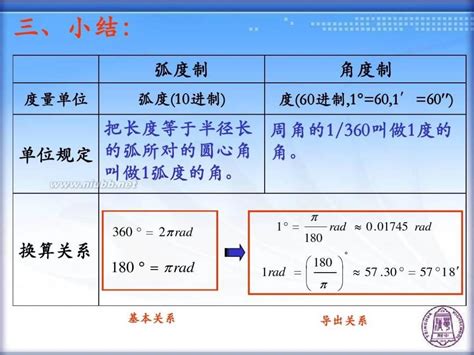
弧度作为角度的一种度量方式，其基础定义是基于圆的周长和半径的比例。具体来说，一个完整的圆周角等于2π弧度。这个定义与常规的度数表示法（360度等于一个圆周角）有所不同，但两者在数学上是等价的，只是表现形式不同。为了理解这一点，我们可以想象一个半径为r的圆，其周长为2πr。如果我们把圆的周长分成若干等份，每一份的长度就对应着相应的弧度。例如，圆周的1/4长度（即半径的π倍）对应的是90度的角，但在弧度制中，这个角就是π/2弧度。

弧度制的优点在于它与圆的几何性质紧密相连，使得许多数学公式和定理在弧度制下更加简洁和直观。特别是在处理三角函数时，弧度制显得尤为重要。三角函数如正弦、余弦和正切等，在弧度制下具有许多重要的性质和恒等式，这些在度数制下则显得复杂和难以记忆。例如，正弦函数和余弦函数的周期在弧度制下恰好是2π，这一特性使得周期函数的分析和处理变得更加简单。

此外，弧度制在物理学中也有广泛的应用。在力学、电磁学和量子力学等领域中，许多物理现象和规律都涉及到圆周运动和周期变化，这些现象和规律在弧度制下更容易描述和理解。例如，在力学中，质点的圆周运动可以用角速度和角加速度来描述，这些物理量在弧度制下具有明确的定义和计算公式。在电磁学中，交流电的周期和频率等参数也与弧度制密切相关。量子力学中的波函数和相位等概念也涉及到弧度制的应用。

除了在数学和物理学中的应用外，弧度制还在计算机科学和工程学中发挥着重要作用。在计算机图形学和计算机视觉中，处理图像的旋转、缩放和变换等操作时需要用到弧度制来表示旋转角度。在工程学中，机械设计、航空航天和自动化控制等领域也涉及到许多与圆周运动和角度计算相关的问题，这些问题同样需要用到弧度制来解决。

为了加深对弧度制的理解，我们可以举几个具体的例子来说明其在不同领域中的应用。在三角函数的教学中，教师可以利用弧度制来引导学生发现正弦函数和余弦函数的周期性和对称性等特点。在物理实验中，学生可以通过测量质点的圆周运动来验证角动量守恒定律和动能定理等物理规律。在计算机图形学的应用中，开发人员可以利用弧度制来实现图像的旋转和缩放等操作，从而创作出丰富多彩的视觉效果。

值得注意的是，虽然弧度制在数学和物理学中具有广泛的应用和优点，但在某些场合下我们仍然需要使用度数制来表示角度。例如，在日常生活中我们习惯于用度数来表示温度的变化和地理坐标的方位等。此外，在某些特定的工程应用中，如建筑设计和机械设计等，也需要用到度数制来表示角度和倾斜度等参数。因此，在实际应用中我们需要根据具体情况选择合适的角度度量方式。

在学习弧度制时，我们还需要注意一些常见的误区和易混淆点。首先，弧度不是单位，而是一个无量纲的量。这意味着弧度本身并不表示任何具体的物理量或单位，而只是角度的一种度量方式。其次，弧度与度数之间的转换需要用到特定的公式和比例关系，这些公式和比例关系必须熟练掌握并正确应用。最后，在处理与角度相关的计算问题时，我们需要根据题目要求选择合适的角度度量方式，并正确运用相关的数学公式和定理进行计算。

综上所述，弧度作为角度的一种度量方式在数学和物理学中具有广泛的应用和重要性。通过深入理解弧度的定义、性质和应用场景，我们可以更好地掌握相关的数学知识和物理规律，并在实际应用中灵活运用这些知识和规律来解决各种问题。同时，我们也需要注意避免一些常见的误区和易混淆点，以确保计算的准确性和可靠性。

在实际应用中，我们还需要注意弧度制与其他角度度量方式之间的转换关系。虽然弧度制在数学和物理学中具有许多优点和应用场景，但在某些特定场合下我们仍然需要使用其他角度度量方式来表示角度。因此，我们需要熟练掌握弧度制与其他角度度量方式之间的转换公式和比例关系，以便在实际应用中根据需要进行灵活转换。

最后，需要强调的是，在学习和应用弧度制时我们应该注重理论与实践的结合。通过理论学习和实践操作相结合的方式，我们可以更好地理解和掌握弧度制的相关知识和应用技能，并在实际应用中不断提高自己的能力和水平。同时，我们也应该注重与其他学科和领域的交叉融合和创新发展，以推动弧度制在数学、物理学以及其他相关领域中的更广泛应用和发展。