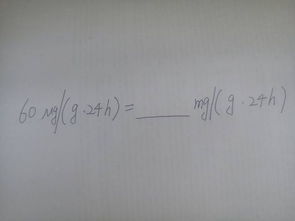揭秘:椭圆周长公式的神奇奥秘
椭圆是一种特殊的几何形状,在数学、物理、工程等多个领域都有着广泛的应用。了解椭圆的周长公式,对于深入研究这一形状的性质及其应用具有重要意义。本文将详细介绍椭圆的周长公式,并探讨其推导过程和相关应用,以帮助读者更好地理解和应用这一知识点。
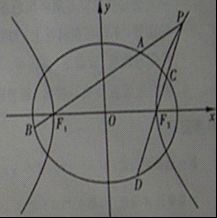
椭圆是平面上所有与两个定点F1和F2的距离之和等于常数(且大于F1F2)的点的轨迹。这两个定点F1和F2被称为椭圆的焦点,而常数则被称为椭圆的长轴长。椭圆的长轴和短轴分别垂直于椭圆的两个对称轴,且长轴长大于短轴长。在椭圆上任取一点P,连接PF1和PF2,则PF1+PF2等于椭圆的长轴长。

椭圆的周长,即椭圆边界线的长度,是一个复杂的数学问题。与圆的周长公式C=2πr相比,椭圆的周长没有如此简洁的表达式。然而,数学家们通过不断努力,已经得出了多种计算椭圆周长的近似公式。其中,较为常用的是拉马努金公式和椭圆周长的第二近似公式。

拉马努金公式是由印度数学家拉马努金提出的,用于计算椭圆的周长。该公式利用了椭圆的半长轴a、半短轴b以及焦点到椭圆上任一点的距离之和(即长轴长)的性质。拉马努金公式为:C≈π[3(a+b)-(a-b)^3/(10a+10√(a^2-b^2)+b)]。这个公式具有较高的精度,适用于大多数椭圆的周长计算。
除了拉马努金公式外,还有椭圆周长的第二近似公式。该公式利用了椭圆的半长轴a、半短轴b以及椭圆的离心率e的性质。椭圆的离心率e定义为e=√(1-(b/a)^2),它反映了椭圆形状扁平的程度。当e=0时,椭圆变为圆;当e接近1时,椭圆变得非常扁平。椭圆周长的第二近似公式为:C≈π[a+b+(a-b)^2/(2√(ab)+10(a√(1-(b/a)^2)+b))]。这个公式虽然精度稍逊于拉马努金公式,但计算过程相对简单,因此在某些场合下也具有一定的应用价值。
在推导椭圆周长公式的过程中,我们需要注意到椭圆形状的特殊性。与圆相比,椭圆在x轴和y轴方向上的尺度是不同的,这导致了椭圆周长计算的复杂性。为了得到精确的椭圆周长公式,我们需要对椭圆进行深入的几何分析,并利用微积分等数学工具进行推导。
拉马努金公式和椭圆周长的第二近似公式都是通过数学近似方法得到的。这些方法利用了椭圆的几何性质和数学表达式,通过一定的数学变换和近似处理,得到了椭圆周长的近似值。虽然这些公式无法给出椭圆周长的精确值,但它们在大多数情况下都具有足够的精度,可以满足实际应用的需求。
椭圆的周长公式在多个领域都有着广泛的应用。在物理学中,椭圆轨道是行星和卫星等天体运动的重要特征之一。了解椭圆的周长公式,有助于我们更准确地描述和预测这些天体的运动轨迹。在工程学中,椭圆形状常用于设计各种机械零件和构件,如轴承、齿轮等。通过计算椭圆的周长,我们可以得到这些零件和构件的精确尺寸和形状参数,从而确保它们能够满足设计要求和工作性能。
此外,椭圆的周长公式还在天文学、地理学、生物学等领域发挥着重要作用。在天文学中,椭圆轨道的周长可以帮助我们计算行星和卫星等天体的运动周期和轨道参数。在地理学中,地球的形状可以近似看作一个椭球体,了解椭圆的周长公式有助于我们更准确地测量地球的大小和形状。在生物学中,某些生物体的形状也呈现出椭圆的特征,如某些植物的叶子和果实等。通过计算这些生物体的椭圆周长,我们可以得到它们的尺寸和形状参数,从而更深入地了解它们的生长和发育过程。
总之,椭圆的周长公式是一个重要的数学知识点,在多个领域都有着广泛的应用。通过了解椭圆的周长公式及其推导过程和相关应用,我们可以更好地理解和应用这一知识点,为解决实际问题提供有力的数学支持。
在实际应用中,我们需要注意选择合适的椭圆周长公式进行计算。对于精度要求较高的场合,可以选择拉马努金公式进行计算;对于计算过程要求简单的场合,可以选择椭圆周长的第二近似公式进行计算。同时,我们还需要注意椭圆周长公式的适用范围和限制条件,以确保计算结果的准确性和可靠性。
此外,随着数学和计算机技术的不断发展,人们也在不断探索更加精确和高效的椭圆周长计算方法。这些新方法可能涉及更复杂的数学理论和算法设计,但它们的出现将为我们解决椭圆周长计算问题提供更加便捷和有效的途径。
综上所述,椭圆的周长公式是一个重要的数学知识点,在多个领域都有着广泛的应用。通过深入了解椭圆的周长公式及其推导过程和相关应用,我们可以更好地掌握这一知识点,为解决实际问题提供有力的数学支持。同时,我们也需要不断关注数学和计算机技术的发展动态,以探索更加精确和高效的椭圆周长计算方法。
- 上一篇: 揭秘:如何在QQ上与好友轻松建立专属密友关系
- 下一篇: H3C路由器如何进行设置?
-
 正三角形的周长该如何计算?资讯攻略10-29
正三角形的周长该如何计算?资讯攻略10-29 -
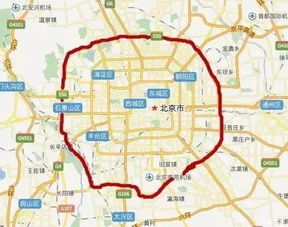 探索北京环路奥秘:二环至六环的周长全揭秘资讯攻略11-02
探索北京环路奥秘:二环至六环的周长全揭秘资讯攻略11-02 -
 揭秘卷积运算:深度学习与图像处理背后的神奇公式资讯攻略10-26
揭秘卷积运算:深度学习与图像处理背后的神奇公式资讯攻略10-26 -
 揭秘:用三角形三边长轻松求解面积的秘密方法资讯攻略11-25
揭秘:用三角形三边长轻松求解面积的秘密方法资讯攻略11-25 -
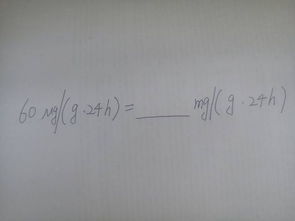 微克与毫克:揭秘它们之间的神奇换算公式!资讯攻略12-07
微克与毫克:揭秘它们之间的神奇换算公式!资讯攻略12-07 -
 揭秘:成绩到等位分的神奇换算公式资讯攻略11-18
揭秘:成绩到等位分的神奇换算公式资讯攻略11-18