揭秘：用三角形三边长轻松求解面积的秘密方法

在数学领域，求解三角形的面积是一个基础而重要的课题。当我们已知三角形的三边长时，可以利用多种方法来求解其面积，其中海伦公式和余弦定理是两种最为常用的方法。本文将详细介绍这两种方法，并通过实例展示其应用，让读者能够全面了解和掌握已知三角形三边长求面积的技能。

首先，我们来了解一下海伦公式。海伦公式是由古希腊数学家海伦提出的，它适用于任意三角形，只要知道三角形的三边长，就可以利用这个公式求出三角形的面积。海伦公式的表达式为：面积等于根号下s乘以（s-a）（s-b）（s-c），其中s是三角形的半周长，即s等于（a+b+c）/2，a、b、c分别为三角形的三边长。

举个例子，假设我们有一个三角形，其三边长分别为a=5，b=6，c=7。首先，我们需要计算三角形的半周长s，即s=（5+6+7）/2=9。然后，将a、b、c和s的值代入海伦公式中，得到面积S=根号下9乘以（9-5）（9-6）（9-7）=6根号下6。

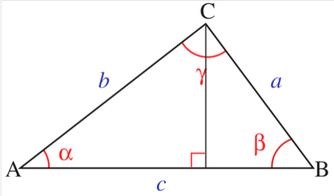
除了海伦公式，我们还可以利用余弦定理来求解三角形的面积。余弦定理是一个描述三角形任意一边的平方等于其他两边的平方和减去这两边与其夹角的余弦的积的2倍的公式。在已知三角形的三边长时，我们可以先利用余弦定理求出三角形的一个内角，然后再利用三角形的面积公式S=1/2absinC（其中C为三角形的一个内角，a、b为与角C相邻的两边）求出三角形的面积。

具体步骤如下：首先，我们可以选择三角形的一个顶点，并设其为C点，与其相邻的两边分别为a和b，夹角为C。然后，我们可以利用余弦定理c²=a²+b²-2abcosC求出cosC的值，即cosC=（a²+b²-c²）/2ab。由于cos²C+sin²C=1，我们可以求出sinC的值，即sinC=根号下（1-cos²C）。最后，将a、b和sinC的值代入三角形的面积公式S=1/2absinC中，就可以求出三角形的面积。

继续以a=5，b=6，c=7的三角形为例，我们可以利用余弦定理求出cosC的值，即cosC=（5²+6²-7²）/（2×5×6）=1/2。然后，我们可以求出sinC的值，即sinC=根号下（1-1/4）=根号下3/2。最后，将a=5，b=6和sinC=根号下3/2的值代入三角形的面积公式S=1/2absinC中，得到面积S=1/2×5×6×根号下3/2=15/2×根号下3，化简后得到面积S=（15根号下3）/2，这个结果与利用海伦公式求出的结果是一致的。

除了海伦公式和余弦定理，我们还可以利用三角形的边长和角度关系来求解三角形的面积。在三角形中，如果已知两边的长度和它们之间的夹角，我们就可以直接利用三角形的面积公式S=1/2absinC来求解。但是，当我们只知道三角形的三边长时，就需要先利用余弦定理或其他方法求出夹角，然后再利用面积公式求解。

在实际应用中，我们可以根据具体情况选择最适合的方法来求解三角形的面积。如果三角形的三边长已知，且我们想要一个简单直接的公式来计算面积，那么海伦公式是一个很好的选择。如果我们想要通过求解夹角来进一步了解三角形的性质，那么利用余弦定理和面积公式可能更为合适。

此外，还有一些特殊情况下的三角形面积求解方法。例如，对于直角三角形，我们可以直接利用勾股定理和直角三角形的面积公式S=1/2ab（其中a、b为直角边）来求解面积。对于等腰三角形和等边三角形，我们也可以利用它们的特殊性质来简化面积的计算过程。

在求解三角形面积的过程中，我们还需要注意一些细节和技巧。例如，在计算过程中要保持精度，避免因为计算误差而导致结果不准确。在利用海伦公式和余弦定理时，要注意公式的适用范围和限制条件。在求解夹角时，要注意角度的取值范围和单位换算等问题。

总之，求解三角形的面积是一个基础而重要的数学技能。当我们已知三角形的三边长时，可以利用海伦公式、余弦定理和面积公式等方法来求解面积。在实际应用中，我们需要根据具体情况选择最适合的方法来求解面积，并注意计算过程中的细节和技巧。通过不断练习和实践，我们可以逐渐掌握这些技能，并在数学学习和实际生活中灵活运用它们。

希望本文能够帮助读者全面了解和掌握已知三角形三边长求面积的技能。在未来的数学学习和实际生活中，当我们遇到需要求解三角形面积的问题时，能够迅速准确地选择最适合的方法来求解面积，为我们的学习和工作提供有力的支持。