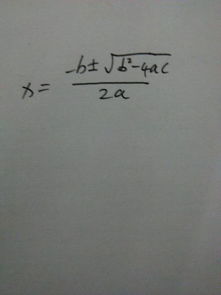揭秘一元二次方程的多样化形态
一元二次方程是数学中非常基础和重要的内容,广泛应用于物理、工程、经济等领域。其一般形式为ax² + bx + c = 0(a ≠ 0),但根据问题的不同背景和解决需求,一元二次方程可以展现出多种不同的形式。本文将详细探讨一元二次方程的多种形式,帮助读者更全面地理解和应用这一知识点。

一、标准形式
一元二次方程的标准形式为ax² + bx + c = 0(a ≠ 0)。这是最基础、最常见的形式。在这个形式中,a、b、c是已知数,x是未知数。解这种方程常用的方法有配方法、公式法和因式分解法。

配方法:通过配方,将原方程转化为完全平方的形式,从而求解。
公式法:使用韦达定理的求根公式x = [-b ± √(b² - 4ac)] / (2a)求解。
因式分解法:当方程左侧可以因式分解时,通过因式分解得到两个一次方程的乘积等于0,从而求解。
二、顶点形式
顶点形式的一元二次方程可以表示为y = a(x - h)² + k,其中(h, k)是抛物线的顶点坐标。这种形式在解析几何中尤为重要,它直接揭示了抛物线的顶点位置。
将顶点形式转化为标准形式,只需展开:
y = a(x - h)² + k = ax² - 2ahx + ah² + k
此时,方程的系数a、b、c分别为:a(保持不变)、b = -2ah、c = ah² + k。
三、交点形式
交点形式主要用于描述抛物线与x轴的两个交点情况,其形式为y = a(x - x1)(x - x2),其中x1和x2是方程ax² + bx + c = 0的两个根。这种形式在求解抛物线与x轴交点时非常方便。
同样,将交点形式转化为标准形式,只需展开:
y = a(x - x1)(x - x2) = ax² - a(x1 + x2)x + ax1x2
由韦达定理知,x1 + x2 = -b/a,x1x2 = c/a,因此方程的系数a、b、c分别为:a(保持不变)、b = -a(x1 + x2) = -b(与标准形式中的b相同)、c = ax1x2 = c(与标准形式中的c相同)。
四、完全平方形式
完全平方形式的一元二次方程形如(x - h)² = k(k ≠ 0)。这种形式虽然看起来不像标准的一元二次方程,但本质上仍然是二次的,因为它可以展开为x² - 2hx + h² - k = 0。
完全平方形式在求解过程中往往能简化计算,特别是在配方和求解抛物线的顶点时。
五、复数形式
在某些情况下,一元二次方程的解可能是复数。当判别式Δ = b² - 4ac < 0时,方程的解为x = [-b ± i√(-Δ)] / (2a),其中i是虚数单位。
复数形式的解在数学和物理学中具有重要意义,尤其是在处理波动、振动和量子物理等问题时。
六、矩阵形式
一元二次方程还可以表示为矩阵形式。例如,对于方程ax² + bx + c = 0,可以构造一个2x2的矩阵A和一个向量b:
A = [ [a, b], [1, 0] ]
b = [c]
[d](这里d为任意实数,因为只要求解x,所以d的取值不影响结果)
然后求解线性方程组Ax = b的解,其中x = [x, y]T,y是一个辅助变量。虽然这种方法在实际计算中不如公式法直接,但它揭示了线性代数与一元二次方程之间的深刻联系。
七、应用形式
在实际应用中,一元二次方程常常以不同的形式出现。例如,在物理学的自由落体问题中,可能会遇到形如s = ut + 0.5gt²的方程,其中s是位移,u是初速度,g是重力加速度,t是时间。这个方程本质上是一个一元二次方程,可以通过整理求解t。
在经济学中,一元二次方程常用于描述成本、收益和利润等经济变量的关系。例如,成本函数C(x) = ax² + bx + c(a > 0)表示生产x单位产品的总成本,其中a、b、c是常数。通过求解这个方程,可以找出使成本最小化的生产量。
八、图形形式
一元二次方程还可以通过图形形式来表示。在平面直角坐标系中,方程ax² + bx + c = 0可以看作是一个抛物线y = ax² + bx + c与x轴的交点问题。通过观察抛物线的形状和位置,可以直观地了解方程的解的情况。
例如,当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。抛物线的对称轴为x = -b/(2a),顶点坐标为(-b/(2a), c - b²/(4a))。这些图形特征对于理解和解决一元二次方程问题非常有帮助。
结语
一元二次方程的多种形式展示了其在数学和实际应用中的广泛性和灵活性。通过掌握这些形式,读者可以更深入地理解一元二次方程的本质和求解方法,从而在数学学习和实际问题解决中更加得心应手。无论是通过标准形式求解方程的根,还是通过顶点形式、交点形式分析抛物线的性质,或者是通过复数形式、矩阵形式探讨方程的深层次联系,一元二次方程都以其独特的魅力吸引着我们去探索和学习。
- 上一篇: 如何在电脑上截取部分图片?
- 下一篇: 创建电脑新拨号连接指南
-
 揭秘:掌握解方程的六大关键公式!资讯攻略11-09
揭秘:掌握解方程的六大关键公式!资讯攻略11-09 -
 揭秘一元云购:高效免费抽奖秘籍资讯攻略10-29
揭秘一元云购:高效免费抽奖秘籍资讯攻略10-29 -
 如何参与网易一元夺宝活动资讯攻略12-09
如何参与网易一元夺宝活动资讯攻略12-09 -
 探索VB编程:绘制迷人的双曲螺线艺术资讯攻略10-29
探索VB编程:绘制迷人的双曲螺线艺术资讯攻略10-29 -
 如何解决一元三次方程?资讯攻略11-09
如何解决一元三次方程?资讯攻略11-09 -
 轻松掌握!一元三次方程的解法大全资讯攻略11-17
轻松掌握!一元三次方程的解法大全资讯攻略11-17