揭秘：掌握解方程的六大关键公式！

在数学学习的旅程中，解方程是每一个学子必经的重要一站。无论是小学数学中的简单加减法方程，还是初中数学中涉及乘法、除法甚至更复杂的方程，掌握一定的公式和技巧都是至关重要的。本文将详细介绍解方程的六个基本公式，并从多个维度进行解析，帮助读者深入理解并灵活应用这些公式。

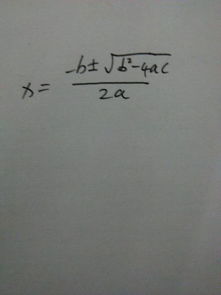
解方程的六个基本公式

1. 一个加数=和-另一个加数

这是解加法方程时最基础的公式。当我们知道两个加数的和以及其中一个加数时，可以通过这个公式轻松求出另一个加数。例如，若已知 x + 5 = 10，要求 x 的值，就可以使用这一公式：x = 10 - 5 = 5。

2. 被减数=差+减数

在减法方程中，这个公式非常有用。它告诉我们，如果知道两个数的差和其中一个数（减数），就可以求出另一个数（被减数）。例如，在方程 x - 7 = 3 中，x 是被减数，7 是减数，3 是差。要找到 x，我们使用公式：x = 3 + 7 = 10。

3. 减数=被减数-差

与上一个公式相对，这个公式用于求解减数。当已知被减数和差时，可以通过这个公式找出减数。例如，在方程 15 - x = 8 中，要找到 x（减数），我们可以使用公式：x = 15 - 8 = 7。

4. 一个因数=积÷另一个因数

乘法方程中，这个公式非常关键。当我们知道两个数的乘积以及其中一个数（因数）时，可以用这个公式求出另一个数（因数）。例如，若 a × x = 24，且已知 a = 6，那么 x = 24 ÷ 6 = 4。

5. 被除数=商×除数

除法方程中，这个公式帮助我们理解被除数、除数和商之间的关系。当我们知道除数和商时，可以用这个公式求出被除数。例如，在方程 x ÷ 4 = 6 中，x 是被除数，4 是除数，6 是商。要找到 x，我们使用公式：x = 6 × 4 = 24。

6. 除数=被除数÷商

与上一个公式相对，这个公式用于求解除数。当已知被除数和商时，可以通过这个公式找出除数。例如，在方程 36 ÷ x = 9 中，要找到 x（除数），我们可以使用公式：x = 36 ÷ 9 = 4。

从多个维度解析这些公式

1. 基础算术运算的深入理解

解方程的六个基本公式，实际上是对基础算术运算（加、减、乘、除）的深入理解和灵活应用。这些公式不仅帮助我们在解方程时找到未知数，也加深了我们对算术运算本质的理解。通过反复使用这些公式，我们可以更加熟练地掌握算术运算，提高计算速度和准确性。

2. 逻辑思维和问题解决能力

解方程不仅仅是简单的数学计算，更是逻辑思维和问题解决能力的体现。当我们面对一个复杂的方程时，需要仔细分析已知条件，确定使用的公式，然后按照逻辑顺序进行计算。这个过程锻炼了我们的逻辑推理能力和问题解决能力，使我们能够更加从容地应对各种数学问题。

3. 数学模型的构建

解方程的过程，实际上是在构建数学模型。我们将实际问题抽象为数学问题，然后利用公式和算法求解。这种将实际问题数学化的能力，是现代科学和技术领域中不可或缺的技能。通过学习解方程，我们培养了构建数学模型的能力，为未来学习和工作打下了坚实的基础。

4. 代数思想的萌芽

在初级数学教育中，解方程是代数思想的萌芽。代数是一种用符号和公式表示数学关系的方法，而解方程正是代数的基础。通过解方程，我们学会了使用符号表示未知数，理解了等式和方程的概念，掌握了代数运算的基本规则。这些知识和技能为后续的代数学习提供了有力的支持。

5. 跨学科应用

解方程不仅在数学学科内部有广泛应用，还跨越到其他学科中。在物理学中，解方程可以帮助我们找到物体的运动规律；在化学中，解方程可以帮助我们计算化学反应的平衡状态；在经济学中，解方程可以帮助我们预测市场趋势。因此，掌握解方程的技能，对于跨学科学习和研究具有重要意义。

实际应用中的注意事项

在解方程时，我们需要注意以下几点：

1. 确保方程正确：在解题前，一定要仔细检查方程是否书写正确，确保没有遗漏或错误的信息。

2. 选择合适的公式：根据方程的特点和已知条件，选择合适的公式进行求解。

3. 注意运算顺序：在进行计算时，要遵循运算的优先级（先乘除后加减，先括号后运算），确保计算结果的正确性。

4. 验证解的正确性：求出解后，一定要将解代入原方程进行验证，确保解的正确性。

5. 培养耐心和细心：解方程需要耐心和细心，尤其是在处理复杂方程时。要保持冷静，逐步进行运算和验证。

结语

解方程的六个基本公式是数学学习中的重要工具，它们不仅帮助我们求解未知数，还培养了我们的逻辑思维、问题解决能力和数学建模能力。通过反复练习和应用这些公式，我们可以更加熟练地掌握数学运算技能，为未来的学习和工作打下坚实的基础。同时，我们也应该意识到解方程在跨学科应用中的重要性，努力将数学知识应用到更广泛的领域中。希望每一位读者都能通过学习和实践，成为数学领域的佼佼者。