阶乘的算法表达式
在数学的奇妙世界里,有一个既简单又充满魅力的概念——阶乘。它虽然只涉及基础的乘法和数字,却能解决许多复杂的问题,是组合数学、概率论等多个领域不可或缺的工具。想象一下,当你想要计算一个事件有多少种不同的排列方式时,阶乘就像是一位默默无闻却神通广大的助手,帮你轻松搞定。那么,什么是阶乘?如何计算阶乘?让我们一起揭开阶乘计算公式的神秘面纱。

阶乘初印象:从定义出发
首先,让我们从阶乘的定义开始。阶乘,用数学符号表示为“!”,读作“factorial”,是指从1乘到某个数n的所有正整数的乘积。换句话说,n的阶乘,记作n!,就是从1一直乘到n的结果。比如,5的阶乘(5!)就是1×2×3×4×5=120。

这里有几个关键点需要注意:
1. 0的阶乘:特别地,0的阶乘(0!)被定义为1。这个规定看似突兀,却有其合理性,它保证了阶乘运算在各种数学公式中的一致性和连贯性。
2. 正整数范围:阶乘通常只定义在正整数上,即n为自然数(包括0)。对于非正整数或非整数,阶乘没有直接的定义。
阶乘计算公式:一步步来
了解了阶乘的基本概念后,我们来看看如何具体计算一个数的阶乘。最直接的方法当然是按照定义,将从1到n的所有整数相乘。但这种方法在n较大时会变得非常繁琐,容易出错。因此,掌握一些阶乘的性质和公式可以大大简化计算过程。
性质一:递归公式
阶乘的一个重要性质是递归性,即n!可以通过(n-1)!来计算:
n! = n × (n-1)!
这个公式告诉我们,要求n的阶乘,可以先求出n-1的阶乘,然后再乘以n。利用这个性质,我们可以从1开始逐步递推,直到求出n的阶乘。例如,计算4!时,可以先计算3!(3! = 3×2×1=6),然后4! = 4×3! = 4×6 = 24。
性质二:分解公式
有时候,我们不需要直接求出n!的确切值,而是需要将其分解为更简单的形式。这时,可以利用阶乘的分解公式:
n! = n × (n-1) × (n-2) × ... × 2 × 1
这个公式直接体现了阶乘的定义,即n!是所有小于等于n的正整数的乘积。
性质三:与组合数的关系
阶乘还与组合数学中的组合数(也称为二项式系数)有着密切的关系。组合数C(n, k)表示从n个不同元素中取出k个元素的组合方式的数量,其计算公式为:
C(n, k) = n! / [k!(n-k)!]
这个公式揭示了阶乘在解决组合问题中的重要作用。通过阶乘,我们可以计算出从一个集合中选择特定数量元素的所有可能方式。
阶乘的应用:从生活到科学
阶乘不仅是一个数学上的概念,它在现实生活和科学研究中也有着广泛的应用。
排列与组合
在排列组合问题中,阶乘是计算不同排列和组合方式数量的基础。比如,在扑克牌游戏中,计算一手牌有多少种不同的排列方式,就需要用到阶乘。同样,在统计学中,计算样本空间的大小也常常涉及阶乘运算。
概率论
在概率论中,阶乘用于计算事件发生的概率。例如,在掷骰子的实验中,计算掷出特定点数序列的概率时,就需要用到阶乘来计算样本空间和特定事件的数量。
物理学与化学
在物理学和化学中,阶乘也扮演着重要角色。比如,在量子力学中,波函数的归一化常数通常涉及阶乘;在化学中,计算分子振动模式的数量时,也需要用到阶乘。
阶乘计算的技巧与工具
虽然阶乘的计算原理相对简单,但当n的值很大时,直接计算会变得非常困难。因此,掌握一些计算技巧和使用合适的工具是非常重要的。
技巧一:利用性质简化计算
如前所述,利用阶乘的递归性质、分解性质以及与组合数的关系,可以大大简化计算过程。此外,还可以利用一些数学恒等式(如斯特林公式)来近似计算大数的阶乘。
技巧二:使用计算器或编程
对于大数的阶乘计算,使用计算器或编程语言中的阶乘函数是最方便的方法。大多数现代计算器都内置了阶乘计算功能,而编程语言(如Python、C等)也提供了相应的库函数来计算阶乘。
注意事项
在计算阶乘时,需要注意数值溢出的问题。当n的值很大时,阶乘的结果可能会超过计算器的存储范围或编程语言的整数类型限制,导致计算结果不准确或程序崩溃。因此,在计算大数的阶乘时,需要选择合适的数据类型和算法来避免溢出问题。
结语
阶乘,这个看似简单的数学概念,却蕴含着丰富的内涵和广泛的应用。从基础的排列组合问题到复杂的科学研究领域,阶乘都发挥着不可替代的作用。通过了解阶乘的定义、计算公式、性质以及应用技巧,我们可以更好地理解和运用这一数学概念,为解决实际问题提供有力的数学工具。希望这篇文章能帮助你深入理解阶乘的奥秘,并在未来的学习和工作中灵活运用它。
- 上一篇: 诲人不倦的深刻含义及实用造句,快速掌握!
- 下一篇: 揭秘:水瓶座(Aquarius)的真正含义
-
 阶乘的定义与公式资讯攻略03-25
阶乘的定义与公式资讯攻略03-25 -
 两个阶乘符号的含义是什么?资讯攻略02-21
两个阶乘符号的含义是什么?资讯攻略02-21 -
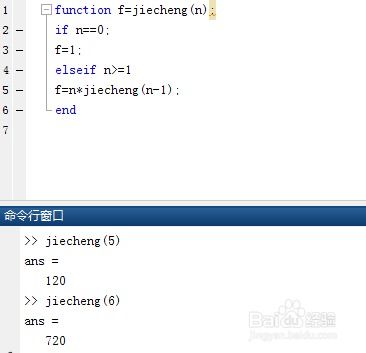 MATLAB中计算阶乘的高效方法大揭秘资讯攻略11-12
MATLAB中计算阶乘的高效方法大揭秘资讯攻略11-12 -
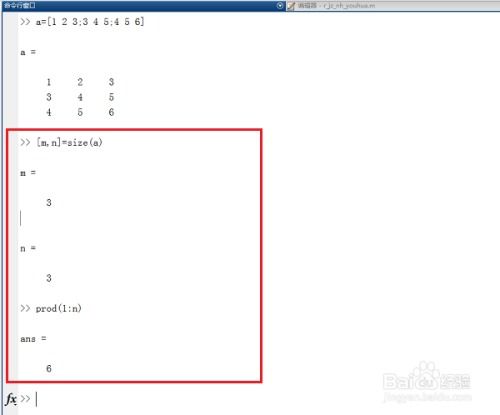 如何在MATLAB中表示阶乘资讯攻略11-09
如何在MATLAB中表示阶乘资讯攻略11-09 -
 求解:好评率算法详解,请帮我计算一下资讯攻略12-05
求解:好评率算法详解,请帮我计算一下资讯攻略12-05 -
 如何在森林舞会之幸运六狮游戏中运用算法技巧?资讯攻略11-01
如何在森林舞会之幸运六狮游戏中运用算法技巧?资讯攻略11-01












