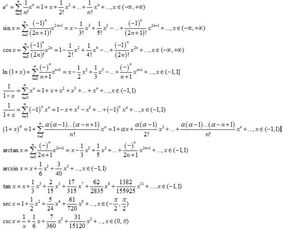阶乘的定义与公式
阶乘的公式是什么,这是数学领域中一个基础而关键的问题。阶乘,作为数学中的一个重要概念,广泛应用于概率论、组合数学以及计算机科学等多个领域。那么,为了深入理解阶乘,我们首先需要明确阶乘的定义及其公式。

阶乘,通常表示为n!,读作“n的阶乘”,是指从1乘到n的所有自然数的乘积。换句话说,一个正整数的阶乘是所有小于及等于该数的正整数的积,并且0的阶乘按照定义是1。这个定义简洁而直观,为我们进一步探讨阶乘的公式奠定了基础。

在数学上,阶乘的公式可以表示为:n! = n × (n-1) × (n-2) × ... × 2 × 1。这个公式清晰地展示了阶乘的计算过程,即从n开始,依次乘以比它小的每一个正整数,直到乘以1为止。例如,5的阶乘(5!)就是5 × 4 × 3 × 2 × 1 = 120。

值得注意的是,阶乘的增长速度非常快。随着n的增大,n!的值会迅速增加,这使得阶乘在处理大数据时显得尤为重要。在计算机科学中,阶乘常用于评估算法的时间复杂度和空间复杂度,因为许多递归算法和动态规划问题都涉及到阶乘的计算。

除了基本的阶乘公式外,还有一些与阶乘相关的公式和性质。例如,阶乘与组合数之间的关系。组合数C(n, k)表示从n个不同元素中取出k个元素的组合方式的数量,其计算公式为C(n, k) = n! / [k!(n-k)!]。这个公式揭示了阶乘在组合数学中的应用,也是概率论和统计学中许多重要概念的基础。
此外,阶乘还与伽马函数有着密切的联系。伽马函数是阶乘函数在复数域上的扩展,它允许我们计算非整数阶乘的值。伽马函数的定义是Γ(z) = ∫0^∞ t^(z-1)e^(-t) dt,对于正整数n,有Γ(n) = (n-1)!。这个性质使得伽马函数在解决涉及阶乘的复杂问题时变得非常有用。
在实际应用中,阶乘的概念和公式被广泛应用于各个领域。在概率论中,阶乘用于计算排列和组合的数量,这是解决许多概率问题的基础。在组合数学中,阶乘是生成函数、递归关系等重要概念的核心。在计算机科学中,阶乘常用于评估算法的性能和优化数据结构。此外,在物理学、化学、生物学等自然科学领域,阶乘也扮演着重要的角色,例如在量子力学中的波函数归一化、化学反应速率计算以及生物种群动态模型等方面。
然而,尽管阶乘的概念和公式在各个领域都有广泛的应用,但在实际计算中,我们也需要注意阶乘的增长速度。由于阶乘的值增长得非常快,因此在处理大数据时,我们可能需要采用特殊的算法或数据结构来存储和计算阶乘的值。例如,使用大数库来处理超过计算机内置数据类型范围的阶乘值,或者采用动态规划的方法来优化阶乘的计算过程。
另外,值得注意的是,阶乘的概念虽然简单直观,但在一些特殊情况下也可能引发误解或混淆。例如,当n为0时,按照阶乘的定义,0! = 1。这个规定可能看起来有些反直觉,但它是为了保持数学上的一致性和便利性而做出的。同样地,在计算组合数时,我们也需要仔细处理n和k的取值范围,以避免出现无效的组合或排列。
综上所述,阶乘的公式是什么这个问题涉及到了阶乘的定义、计算方法、相关性质以及实际应用等多个方面。通过深入理解阶乘的概念和公式,我们可以更好地掌握数学中的这一基础而关键的概念,并将其应用于解决各种实际问题。无论是在概率论、组合数学还是计算机科学等领域,阶乘都扮演着重要的角色,为我们提供了强大的数学工具来解决复杂的问题。因此,掌握阶乘的公式和性质对于提高我们的数学素养和解决实际问题能力具有重要意义。
- 上一篇: 西甲联赛:激战多少轮,冠军花落谁家?
- 下一篇: 揭秘:“draken”一词的真正含义是什么?
-
 阶乘的算法表达式资讯攻略11-30
阶乘的算法表达式资讯攻略11-30 -
 两个阶乘符号的含义是什么?资讯攻略02-21
两个阶乘符号的含义是什么?资讯攻略02-21 -
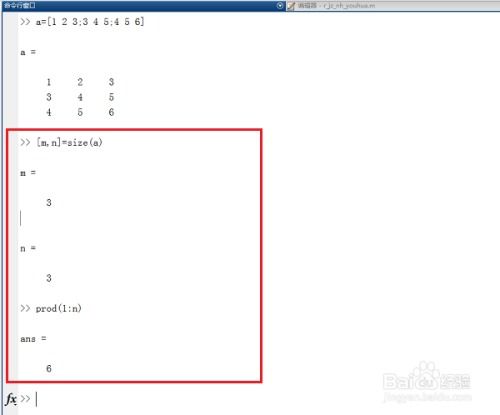 如何在MATLAB中表示阶乘资讯攻略11-09
如何在MATLAB中表示阶乘资讯攻略11-09 -
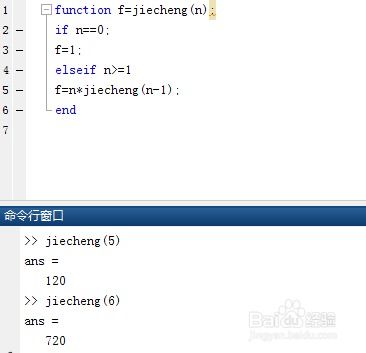 MATLAB中计算阶乘的高效方法大揭秘资讯攻略11-12
MATLAB中计算阶乘的高效方法大揭秘资讯攻略11-12 -
 工程力学中惯性矩的定义和计算公式是什么?资讯攻略02-13
工程力学中惯性矩的定义和计算公式是什么?资讯攻略02-13 -
 cotx的等价公式是什么?资讯攻略02-05
cotx的等价公式是什么?资讯攻略02-05