揭秘棱锥体积的奥秘
在我们探讨几何学的奇妙世界时,经常会遇到各种各样的立体图形,而棱锥便是其中一类既经典又实用的几何体。无论是在日常生活中的建筑设计、工程制图,还是在学术研究的数学物理领域,棱锥都扮演着不可或缺的角色。今天,我们就来详细聊聊一个关于棱锥的基本而重要的问题——棱锥的体积是什么?希望通过这篇文章,你能对这个概念有一个清晰而深入的理解。
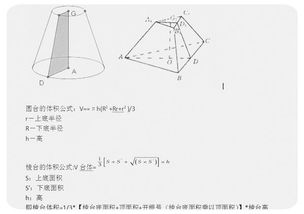
首先,让我们从棱锥的定义开始。棱锥是一种特殊的立体图形,它由一个多边形底面(称为基础面)和与这个底面的每一顶点相连的一组三角形侧面(称为侧面)组成。这些三角形侧面有一个共同的顶点,这个点不位于底面上,我们称之为棱锥的顶点。根据底面的形状不同,棱锥可以进一步分类,比如三角形底面的棱锥称为三棱锥(或四面体),四边形底面的称为四棱锥,以此类推。

那么,如何计算棱锥的体积呢?这里我们需要引入一个关键的概念——高。棱锥的高是从顶点垂直到底面(或底面所在平面)的最短距离。想象一下,如果我们把一个棱锥放在一个水平面上,用一个垂直于水平面的尺子去量从顶点到底面的垂直距离,这个距离就是棱锥的高。
接下来,我们来看看棱锥体积的计算公式。对于任何棱锥,无论其底面形状如何,其体积V都可以通过以下公式计算:
V = (1/3) * 底面积 * 高
这个公式简洁而强大,它告诉我们棱锥的体积是其底面积与高的乘积的三分之一。这个三分之一的比例因子是棱锥体积计算中的一个重要特点,也是与棱柱(另一种常见的立体图形,其体积是底面积与高的直接乘积)相比的一个显著区别。
为了更直观地理解这个公式,我们可以考虑一个简单的例子——三棱锥(四面体)。假设我们有一个底面为等边三角形、边长为a的三棱锥,且其高(从顶点到底面的垂直距离)为h。首先,我们需要计算底面的面积。等边三角形的面积公式是(√3/4)*a²,将a代入公式即可得到底面的面积。然后,我们将这个面积和棱锥的高h代入到棱锥体积的公式中,就可以得到三棱锥的体积为(1/3)*(√3/4)*a²*h。
当然,在实际应用中,棱锥的底面可能并不是简单的等边三角形,而是更复杂的形状,比如矩形、平行四边形甚至是不规则的多边形。但无论底面形状如何复杂,我们都可以通过相应的面积计算公式求出底面的面积,然后再利用棱锥体积的公式进行计算。
除了直接计算外,棱锥的体积还可以通过一些间接的方法求解。比如,如果我们知道一个棱锥可以被分割成若干个小棱锥(这些小棱锥的底面都是原棱锥底面的部分区域,且都共享原棱锥的顶点),那么我们就可以分别计算这些小棱锥的体积,然后将它们相加得到原棱锥的体积。这种方法在处理一些复杂形状的棱锥时特别有用。
此外,棱锥的体积还与其相似的棱锥之间存在一种比例关系。如果两个棱锥是相似的(即它们的底面形状相同且对应边之间的比例是常数),那么它们的体积之比等于它们对应边之比的三次方。这个性质可以用来解决一些与棱锥体积成比例的问题。
在日常生活和工作中,棱锥的体积计算有着广泛的应用。比如,在建筑设计中,工程师需要计算建筑物的某些部分的体积来估算材料用量和成本;在地质勘探中,科学家需要计算地下岩石或矿体的体积来评估资源储量和开采潜力;在物理学中,棱锥的体积概念也被用于解释一些自然现象和物理过程。
最后,值得注意的是,虽然棱锥的体积计算公式看起来很简单,但在实际应用中却需要注意一些细节问题。比如,在计算底面面积时,要确保使用正确的面积公式;在测量棱锥的高时,要确保测量的是从顶点到底面的垂直距离而不是其他形式的距离;在利用相似棱锥的体积比例关系时,要确保两个棱锥确实是相似的且对应边之间的比例是准确的。
总之,棱锥的体积是几何学中的一个重要概念,它不仅具有理论价值,还具有广泛的应用价值。通过理解和掌握棱锥体积的计算方法和相关性质,我们可以更好地理解和解决与棱锥相关的实际问题。希望这篇文章能够帮助你更好地理解棱锥的体积是什么以及如何计算它。在未来的学习和工作中,当你遇到与棱锥体积相关的问题时,不妨回想一下这篇文章的内容,相信你一定能够找到解决问题的线索和方法。
- 上一篇: 揭秘红筹股:定义与魅力何在?
- 下一篇: 桀骜不驯的同义词汇
-
 揭秘正方体体积的求解奥秘资讯攻略11-16
揭秘正方体体积的求解奥秘资讯攻略11-16 -
 揭秘:一吨黄金究竟能占据多大的空间?资讯攻略12-06
揭秘:一吨黄金究竟能占据多大的空间?资讯攻略12-06 -
 排量单位该如何表述?资讯攻略01-09
排量单位该如何表述?资讯攻略01-09 -
 木星与土星:哪个更大?资讯攻略11-08
木星与土星:哪个更大?资讯攻略11-08 -
 揭秘!1立方米究竟等于多少立方厘米?资讯攻略03-10
揭秘!1立方米究竟等于多少立方厘米?资讯攻略03-10 -
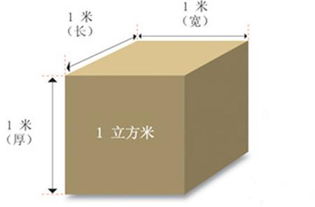 揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03
揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03












