揭秘正方体体积的求解奥秘
正方体体积的计算方法是几何学中的基础内容,对于学习数学、物理以及工程等领域的学生和专业人士来说,掌握这一知识点至关重要。正方体作为一种特殊的三维几何体,其六个面都是正方形,且所有棱长相等。要求出正方体的体积,首先需要明确正方体的基本特征,即它的边长。
在正式讨论正方体体积的计算方法之前,有必要回顾一下体积的定义。体积是三维空间中物体所占的空间大小,通常用立方单位(如立方厘米、立方米等)来表示。对于规则几何体,如正方体,其体积可以通过公式直接计算得出。

正方体的体积计算公式为:体积V等于边长a的三次方,即V=a³。这个公式简洁明了,只要知道正方体的任意一条边的长度,就可以迅速求出其体积。
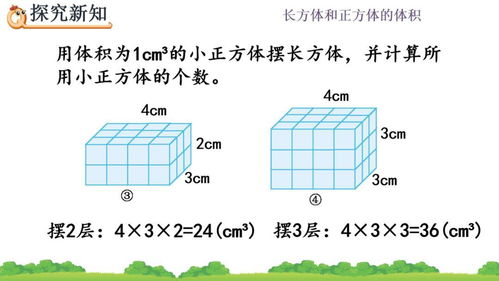
接下来,我们通过一个具体的例子来演示如何应用这个公式。假设有一个正方体,其边长为5厘米。根据正方体体积的计算公式,我们可以将边长5厘米代入公式中,得到体积V等于5³,即125立方厘米。因此,这个正方体的体积是125立方厘米。
为了深入理解正方体体积的计算方法,我们可以从正方体的构造出发进行分析。正方体由六个面组成,每个面都是一个正方形。由于正方体的所有棱长相等,我们可以将正方体看作是由多个小正方体(边长为单位长度)堆叠而成。这些小正方体的数量正好等于大正方体边长的三次方。因此,正方体体积的计算公式V=a³实际上反映了正方体内部小正方体的数量。
此外,正方体体积的计算还可以与其他几何体的体积进行比较和联系。例如,长方体的体积计算公式为V=l×w×h,其中l、w、h分别为长方体的长、宽、高。当长方体的长、宽、高都相等时,它就变成了一个正方体。此时,长方体的体积公式就简化为V=a³,与正方体的体积公式一致。
除了与长方体的联系外,正方体体积的计算还可以与球体的体积进行比较。球体的体积计算公式相对复杂,为V=(4/3)πr³,其中r为球体的半径。虽然正方体和球体的形状截然不同,但它们的体积都与边长的三次方(或半径的三次方)成正比。这反映了三维空间中物体体积增长的一种普遍规律:当物体的尺寸增大时,其体积的增长速度比尺寸的增长速度要快得多。
在实际应用中,正方体体积的计算方法具有广泛的应用价值。例如,在建筑和工程领域,经常需要计算各种几何体的体积,以便进行材料估算和成本分析。正方体作为一种常见的几何体,其体积的计算方法在这些领域中具有重要的实用价值。
此外,在物理学和天文学中,正方体体积的计算方法也具有一定的应用。例如,在研究星系的形状和分布时,科学家们经常将星系近似看作是由多个小正方体组成的网格结构。通过计算这些小正方体的体积和分布,科学家们可以推断出星系的总体形状和性质。
当然,在学习正方体体积的计算方法时,我们也需要注意一些常见的误区和错误。例如,有些学生可能会将正方体的表面积与体积混淆。正方体的表面积是指其所有面的面积之和,而体积则是指其内部所占的空间大小。这两者的计算方法和物理意义都截然不同,因此必须加以区分。
另外,还有一些学生可能会在计算过程中忽略单位换算的问题。在进行正方体体积的计算时,必须确保所使用的边长单位与所求的体积单位相匹配。如果单位不匹配,就需要进行单位换算,以确保计算结果的准确性。
除了上述误区和错误外,还有一些需要注意的问题。例如,在计算过程中要注意保留有效数字,以避免计算结果的精度损失。同时,也要注意检查计算过程中的每一步是否都正确无误,以确保最终结果的准确性。
综上所述,正方体体积的计算方法是几何学中的基础内容,具有广泛的应用价值。通过掌握正方体体积的计算方法,我们可以更好地理解和应用几何学知识,为学习和工作打下坚实的基础。同时,我们也需要注意避免常见的误区和错误,以确保计算结果的准确性和可靠性。
在未来的学习和工作中,我们将继续遇到各种与正方体体积计算相关的问题和挑战。通过不断学习和实践,我们可以不断提高自己的数学素养和解决问题的能力,为更好地应对这些挑战做好准备。希望每一位读者都能通过本文的介绍和讨论,对正方体体积的计算方法有更深入的了解和认识。
- 上一篇: 爱奇艺APP如何下载电视剧?
- 下一篇: 完美自制珍珠奶茶的详细步骤
-
 立方体体积的计算方法资讯攻略10-30
立方体体积的计算方法资讯攻略10-30 -
 立方体体积的计算公式是什么?资讯攻略12-06
立方体体积的计算公式是什么?资讯攻略12-06 -
 揭秘棱锥体积的奥秘资讯攻略11-30
揭秘棱锥体积的奥秘资讯攻略11-30 -
 揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03
揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03 -
 揭秘YSZNWZAN的神秘重复:这句话背后的深意,求解!资讯攻略12-07
揭秘YSZNWZAN的神秘重复:这句话背后的深意,求解!资讯攻略12-07 -
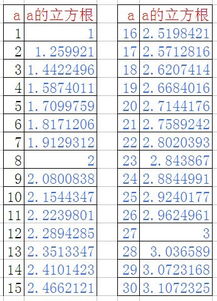 探索数学之美:1至30的数字立方根全览资讯攻略12-03
探索数学之美:1至30的数字立方根全览资讯攻略12-03










