等腰三角形边长计算全攻略

等腰三角形作为一种基本的几何图形，在数学、物理学以及工程学等多个领域都有着广泛的应用。在了解等腰三角形的性质时，掌握其边长公式显得尤为重要。本文将从等腰三角形的定义、基本性质、边长公式的推导和应用四个方面，详细阐述等腰三角形的边长计算方法。

一、等腰三角形的定义

等腰三角形是指两边长度相等的三角形。在三角形ABC中，如果AB=AC（或BC=BA，或CA=CB），则称三角形ABC为等腰三角形。其中，相等的两边被称为等腰三角形的腰，第三边则被称为底边。此外，等腰三角形的两个底角也是相等的，这是等腰三角形的一个重要性质。

二、等腰三角形的基本性质

1. 等腰三角形的两个底角相等：

根据等腰三角形的定义，如果AB=AC，则∠B=∠C。这个性质可以通过全等三角形的判定定理来证明。

2. 等腰三角形的中线、高线和角平分线重合：

在等腰三角形中，从顶点到底边中点的线段（中线）、从顶点到底边的垂线段（高线）以及顶角的角平分线互相重合。这个性质是等腰三角形特有的，它简化了等腰三角形的很多问题。

3. 等腰三角形的周长：

等腰三角形的周长是其三条边之和。由于等腰三角形有两边相等，所以周长可以表示为2a+b（其中a为腰长，b为底边长）。

三、等腰三角形的边长公式推导

在等腰三角形中，由于两边相等，我们可以利用这一性质和一些基本的几何知识来推导边长公式。以下是几种常见的边长公式推导方法：

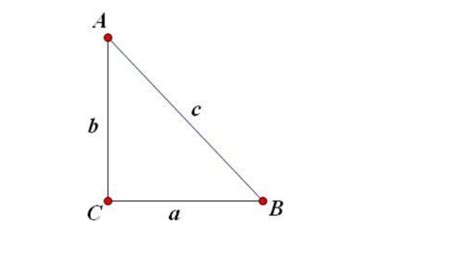
1. 利用勾股定理：

在直角三角形中，勾股定理（a²+b²=c²）是一个基本的定理。在等腰直角三角形中，如果两条腰长均为a，底边长为b，则根据勾股定理，我们有a²+a²=b²，即2a²=b²，从而得出b=√(2)a。这是一个特殊的等腰三角形边长公式。

2. 利用余弦定理：

对于一般的等腰三角形，我们可以利用余弦定理来推导边长公式。设等腰三角形的两条腰长分别为a，底边长为b，顶角为θ，则根据余弦定理，我们有a²=b²/2+a²/2-2*(b/2)*(a/2)*cosθ。化简后得到cosθ=(b²/2a²-1)/(b/a)。如果我们知道顶角和一条腰长，就可以通过这个公式求出底边长。

3. 利用等腰三角形的对称性：

在等腰三角形中，如果我们知道底边长和底边上的高（或中线、角平分线），我们也可以利用等腰三角形的对称性来求解腰长。设底边长为b，高为h，则根据勾股定理，我们有a²=h²+(b/2)²。如果我们知道底边长和高，就可以通过这个公式求出腰长。

四、等腰三角形的边长公式应用

等腰三角形的边长公式在解决实际问题中有着广泛的应用。以下是几个具体的例子：

1. 工程问题：

在建筑工程中，我们经常需要计算一些与等腰三角形相关的尺寸。比如，在设计一个等腰三角形的屋顶时，我们需要知道屋顶的高度、宽度以及斜边的长度。这些都可以通过等腰三角形的边长公式来计算。

2. 物理问题：

在物理学中，等腰三角形也经常出现。比如，在力学问题中，我们经常需要计算一些与等腰三角形相关的力和力矩。这些计算都需要用到等腰三角形的边长公式。

3. 几何问题：

在几何学中，等腰三角形是一个重要的研究对象。我们经常需要证明一些与等腰三角形相关的定理和性质，这些都需要用到等腰三角形的边长公式。比如，在证明等腰三角形的中线、高线和角平分线重合时，我们就需要用到边长公式来计算相关的边长和角度。

以下是一个具体的应用例子：

例子：已知等腰三角形的底边长为8cm，底边上的高为6cm，求腰长。

解：设等腰三角形的腰长为a，底边长为b，高为h。根据题目条件，我们有b=8cm，h=6cm。

根据勾股定理，我们有a²=h²+(b/2)²。将已知的b和h代入公式，得到a²=6²+(8/2)²=36+16=52。

所以，a=√(52)=2√(13)cm。

因此，等腰三角形的腰长为2√(13)cm。

在实际应用中，我们可能需要根据已知条件选择适当的边长公式进行计算。比如，如果已知顶角和一条腰长，我们可以选择利用余弦定理来计算底边长；如果已知底边长和高，我们可以选择利用