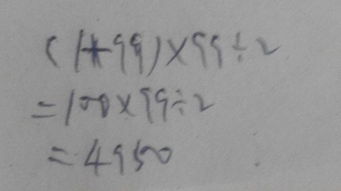求解1至99累加和的过程及结果
在数学的世界里,有一个古老而有趣的问题:从1加到99,这些数字的总和是多少?这个问题看似简单,却蕴含着深刻的数学原理和巧妙的解题技巧。今天,我们就来一起探索这个问题的解答过程,不仅计算出总和,还要理解背后的数学逻辑和思维方法。

首先,我们直接面对问题:从1加到99,即1+2+3+...+99,要求出这些数字的总和。最直接的方法是逐个相加,但这种方法繁琐且容易出错,不适合大范围的数字求和。因此,我们需要寻找一种更简洁、高效的解题方法。
高斯求和法为我们提供了这样一种思路。高斯是德国的著名数学家,他在童年时期就展现出了非凡的数学天赋。据说,高斯在上小学时,老师出了一道题:计算从1到100的所有整数的和。其他孩子还在逐个相加时,高斯已经迅速给出了答案:5050。他是怎么做到的呢?
高斯采用的是一种巧妙的配对方法。他将1和100、2和99、3和98等数字两两配对,每一对的和都是相同的(在这个例子中是101)。由于1到100共有100个数字,可以配成50对,所以总和就是50对×101=5050。
虽然我们的问题是求从1加到99的和,但高斯求和法的原理同样适用。我们可以将1和99、2和98、...、49和51配对,每一对的和都是100。注意,这里我们忽略了中间的50,因为它没有配对伙伴。所以,从1加到99的总和就是49对×100+50。
计算过程如下:
1+2+3+...+99
=(1+99)+(2+98)+...+(49+51)+50
=100×49+50
=4900+50
=4950
所以,从1加到99的总和是4950。
除了高斯求和法外,我们还可以使用数学公式来求解这个问题。等差数列求和公式是一个非常有用的工具。等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列。在这个问题中,从1加到99就是一个等差数列,公差为1。
等差数列的求和公式为:Sn=n/2×(a1+an),其中Sn是前n项和,a1是首项,an是第n项。在我们的问题中,n=99(因为有99个数字),a1=1(首项是1),an=99(第99项是99)。
将这些值代入公式中,我们得到:
Sn=99/2×(1+99)
=99/2×100
=4950
再次验证了我们的结果:从1加到99的总和是4950。
这个问题不仅是一个简单的数学计算题,它还蕴含了深刻的数学思想和方法。高斯求和法教会我们如何运用配对和对称性的思想来简化问题;等差数列求和公式则是一个通用的工具,可以应用于更广泛的等差数列求和问题中。
此外,这个问题还启示我们:在面对复杂问题时,要善于寻找规律、运用技巧来简化问题。在数学中,这种思维方法非常重要;在现实生活中,同样如此。只有掌握了正确的方法和技巧,我们才能更加高效地解决问题、创造价值。
进一步拓展这个问题,我们还可以思考一些变体。比如:如果从1加到某个未知数n的和已知,能否反推出n的值?或者:能否将高斯求和法或等差数列求和公式应用于其他类似的求和问题中?这些问题都值得我们深入思考和探索。
在数学的世界里,每一个问题都是一个宝藏箱,等待着我们去挖掘其中的宝藏。从1加到99这个问题虽然简单,但它却为我们打开了一扇通往数学奥秘的大门。通过这个问题,我们不仅学会了如何计算从1加到99的和,更重要的是,我们学会了如何运用数学思维和技巧来解决问题、探索未知。
最后,让我们再次回顾一下这个问题的解答过程:首先,我们采用了高斯求和法,通过配对和对称性的思想简化了问题;然后,我们使用了等差数列求和公式进行了验证和拓展。在这个过程中,我们不仅得到了问题的答案,更重要的是,我们收获了数学思维和解决问题的能力。这些能力和思维方法将伴随我们一生,成为我们面对挑战、创造未来的有力武器。
- 上一篇: 揭秘:我国古代对木星的神秘称谓是什么?
- 下一篇: 掌握高效秘诀:如何大幅提升你的办事效率
-
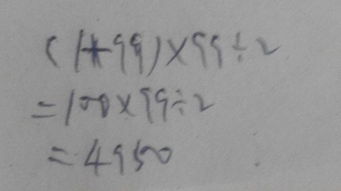 计算1至99的总和是多少资讯攻略02-27
计算1至99的总和是多少资讯攻略02-27 -
 一键上传99张图片至微信的教程资讯攻略11-22
一键上传99张图片至微信的教程资讯攻略11-22 -
 揭秘:根号576再开方的结果是多少?资讯攻略11-30
揭秘:根号576再开方的结果是多少?资讯攻略11-30 -
 揭秘:22的2次方计算结果是多少?资讯攻略11-12
揭秘:22的2次方计算结果是多少?资讯攻略11-12 -
 高等数学入门:曲线拐点的定义与求解方法资讯攻略11-08
高等数学入门:曲线拐点的定义与求解方法资讯攻略11-08 -
 揭秘!如何获取《天之痕》中的珍稀99套轩辕伏魔录?资讯攻略11-08
揭秘!如何获取《天之痕》中的珍稀99套轩辕伏魔录?资讯攻略11-08