高等数学入门:曲线拐点的定义与求解方法
高等数学入门——曲线拐点的定义及求法

在数学中,特别是高等数学的学习过程中,曲线的拐点是一个重要的概念。拐点,顾名思义,是曲线上一个方向的凹凸性发生变化的点。理解并掌握拐点的定义及其求法,对于分析函数图像的性质具有重要意义。下面,我们将深入探讨曲线拐点的定义及求法。
一、拐点的定义
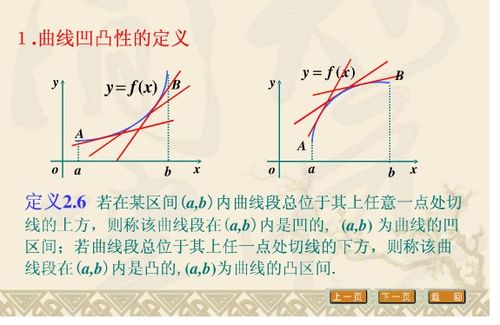
拐点,又称为反曲点,是曲线上一个点,该点两侧的切线斜率符号相反,即函数在该点两侧的凹凸性发生变化。具体来说,设函数y=f(x)在区间I上连续,如果对I中的任意两点x1和x2,当x1(f(x1)+f(x2))/2,那么称f(x)在区间I上是凸的(或向下凹的)。
若函数y=f(x)在点c的左邻域内是凹的,在右邻域内是凸的,则称点c为函数y=f(x)的拐点。反过来,若函数y=f(x)在点c的左邻域内是凸的,在右邻域内是凹的,点c同样也称为函数y=f(x)的拐点。如果函数f(x)在区间I的每一点上都是凹的或凸的,则称f(x)在I上是凹函数或凸函数。这时I上不存在拐点。
二、拐点的求法
1. 二阶导数法
二阶导数法是求拐点的一种常用方法。若函数y=f(x)在区间I上二阶可导,且f''(x)在区间I上不变号,则f(x)在区间I上没有拐点。若f''(x)在I上变号,则变号点即为拐点。
具体来说,如果在某点x0处,二阶导数f''(x0)=0,且在x0的两侧f''(x)的符号不同,则(x0,f(x0))是拐点。需要注意的是,f''(x0)=0并不是判断拐点的充分条件,还需要检查f''(x)在x0两侧的符号是否不同。
示例:
考虑函数f(x)=x^3。其一阶导数为f'(x)=3x^2,二阶导数为f''(x)=6x。
令f''(x)=0,解得x=0。
考察f''(x)在x=0两侧的符号:
当x<0时,f''(x)=6x<0;
当x>0时,f''(x)=6x>0。
因此,f''(x)在x=0两侧符号不同,所以(0,f(0))=(0,0)是拐点。
2. 三阶导数法
对于某些复杂函数,直接求二阶导数可能比较困难,此时可以考虑利用三阶导数来判断拐点。
如果f''(x)在某点x0处为零,且f'''(x0)≠0,则当f'''(x0)>0时,f''(x)在x0左侧为负,在x0右侧为正,即(x0,f(x0))为拐点;当f'''(x0)<0时,f''(x)在x0左侧为正,在x0右侧为负,即(x0,f(x0))也为拐点。
示例:
考虑函数f(x)=x^4-x^2。其一阶导数为f'(x)=4x^3-2x,二阶导数为f''(x)=12x^2-2,三阶导数为f'''(x)=24x。
令f''(x)=0,解得x=±√(1/6)和x=0(但由于x=0处f'''(x)=0,所以此处需要进一步分析,或利用其他方法判断)。
对于x=±√(1/6):
f'''(±√(1/6))=±4√6≠0,且f''(x)在x=±√(1/6)两侧符号不同,所以(±√(1/6),f(±√(1/6)))是拐点。
3. 几何法
对于一些简单的函数图像,可以直接通过观察函数图像来找出拐点。拐点的几何特征是:在该点处
-
 揭秘:轻松求解曲线拐点的绝妙方法资讯攻略11-15
揭秘:轻松求解曲线拐点的绝妙方法资讯攻略11-15 -
 拐点:是点还是坐标的辨析资讯攻略12-07
拐点:是点还是坐标的辨析资讯攻略12-07 -
 揭秘函数拐点:它们为何重要且如何识别?资讯攻略10-24
揭秘函数拐点:它们为何重要且如何识别?资讯攻略10-24 -
 揭秘圆锥曲线的神秘第二定义资讯攻略03-07
揭秘圆锥曲线的神秘第二定义资讯攻略03-07 -
 等腰三角形已知底和高,如何求解其边长?资讯攻略10-28
等腰三角形已知底和高,如何求解其边长?资讯攻略10-28 -
 什么是OpenCV中的norm函数?范数求解全解析资讯攻略11-04
什么是OpenCV中的norm函数?范数求解全解析资讯攻略11-04