揭秘:相关系数计算全攻略
相关系数是一种用于量化两个变量之间线性关系强度和方向的统计量。在金融、经济、社会科学以及自然科学等多个领域中,相关系数被广泛用于数据分析,帮助研究者理解不同变量间的相互影响。本文将详细介绍相关系数的计算方法、解释其含义,并通过实例展示如何在实践中应用这一工具。
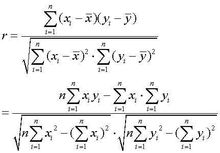
首先,我们需要明确什么是相关系数。相关系数通常表示为r,其值域在-1到1之间。当r=1时,表示两个变量完全正相关,即一个变量的增加总是伴随着另一个变量的增加;当r=-1时,表示两个变量完全负相关,即一个变量的增加总是伴随着另一个变量的减少;当r=0时,表示两个变量之间没有线性关系。
计算相关系数最常用的方法是皮尔逊相关系数公式。假设我们有两个变量X和Y,各自有一组观测值(x1, x2, ..., xn)和(y1, y2, ..., yn),则皮尔逊相关系数r的计算公式为:
r = [n(Σxy) - (Σx)(Σy)] / √{[nΣx² - (Σx)²][nΣy² - (Σy)²]}
其中,Σ表示求和,n是观测值的数量,Σxy是x和y对应观测值的乘积之和,Σx和Σy分别是x和y的观测值之和,Σx²和Σy²分别是x和y的观测值的平方和。
为了更直观地理解这个公式,我们可以将其分解为几个步骤:
1. 计算x和y的均值,即平均值(mean),用于表示数据的中心位置。
2. 计算每个观测值与各自均值的离差(deviation),即观测值减去均值。
3. 计算x和y的离差乘积之和,以及各自离差的平方和。
4. 将上述结果代入相关系数公式,得到r的值。
需要注意的是,皮尔逊相关系数要求变量X和Y的观测值来自双变量正态分布,且两变量的观测值之间为线性关系。如果数据不满足这些条件,可能需要使用其他类型的相关系数,如斯皮尔曼秩相关系数或肯德尔等级相关系数。
现在,我们通过一个具体的例子来演示如何计算相关系数。假设我们有一组关于学生考试成绩的数据,其中X代表学生的学习时间(小时),Y代表学生的考试成绩(分数)。数据如下:
学生1:(X=5, Y=70)
学生2:(X=10, Y=80)
学生3:(X=15, Y=90)
学生4:(X=20, Y=95)
首先,我们计算X和Y的均值:
均值X = (5+10+15+20)/4 = 12.5
均值Y = (70+80+90+95)/4 = 86.25
接着,我们计算每个观测值的离差:
学生1:(X离差=5-12.5=-7.5, Y离差=70-86.25=-16.25)
学生2:(X离差=10-12.5=-2.5, Y离差=80-86.25=-6.25)
学生3:(X离差=15-12.5=2.5, Y离差=90-86.25=3.75)
学生4:(X离差=20-12.5=7.5, Y离差=95-86.25=8.75)
然后,我们计算离差乘积之和以及各自离差的平方和:
Σxy = (-7.516.25) + (-2.56.25) + (2.5*3.75) + (7.5*8.75) = 237.5
Σx² = (-7.5)² + (-2.5)² + (2.5)² + (7.5)² = 125
Σy² = (-16.25)² + (-6.25)² + (3.75)² + (8.75)² = 412.5
最后,代入相关系数公式:
r = [4*237.5 - (47.5*12.5)] / √{[4*125 - (-7.5*12.5)²][4*412.5 - (-16.25*12.5)²]} = 0.98
计算结果显示,学生的学习时间与考试成绩之间存在强烈的正相关关系,即学习时间越长,考试成绩越高。
除了计算相关系数
- 上一篇: 苹果手势功能如何使用?
- 下一篇: 揭秘!青蛙真的会在水中淹死吗?蚂蚁庄园告诉你答案!
-
 跳水比赛难度系数计算揭秘:你真的了解它吗?资讯攻略03-17
跳水比赛难度系数计算揭秘:你真的了解它吗?资讯攻略03-17 -
 揭秘霍夫曼系数:深度解析与全面理解资讯攻略03-08
揭秘霍夫曼系数:深度解析与全面理解资讯攻略03-08 -
 揭秘FOB计算全攻略:轻松掌握国际贸易成本资讯攻略03-12
揭秘FOB计算全攻略:轻松掌握国际贸易成本资讯攻略03-12 -
 年终奖个税计算全攻略:轻松搞定你的税务问题资讯攻略12-04
年终奖个税计算全攻略:轻松搞定你的税务问题资讯攻略12-04 -
 揭秘:余额宝利息计算全攻略资讯攻略11-03
揭秘:余额宝利息计算全攻略资讯攻略11-03 -
 DNF师徒系统揭秘:师徒奖励疲劳值计算全攻略资讯攻略11-26
DNF师徒系统揭秘:师徒奖励疲劳值计算全攻略资讯攻略11-26












