如何轻松计算置信区间?
置信区间是统计学中用来估计总体参数的一种方法,它给出了一个范围,表明总体参数有一定概率落在这个范围内。这种估计方法对于理解数据的可靠性、进行决策分析和科学研究至关重要。本文将从置信区间的定义、计算方法、影响因素以及实际应用等多个维度来详细阐述如何计算置信区间。
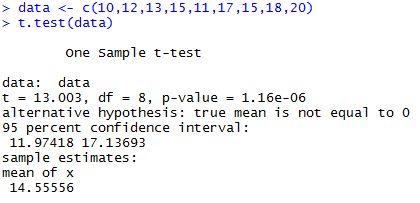
置信区间的定义
在统计学中,一个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。简单来说,置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信区间给出的是被测量参数的测量值的可信程度,这个概率被称为置信水平。

置信区间通常表示为[a, b],其中a和b是置信区间的下限和上限。例如,如果在一次大选中某人的支持率为55%,而置信水平为95%的置信区间是(50%,60%),那么他的真实支持率有95%的概率落在50%和60%之间。

置信区间的计算方法
置信区间的计算方法依赖于样本数据、所选择的置信水平和总体分布的特性。以下是计算置信区间的一般步骤:
1. 确定置信水平:通常选择的置信水平有90%、95%或99%。置信水平越高,置信区间越宽。
2. 收集样本数据:包括样本均值、样本标准差和样本大小(n)。样本均值是样本数据的平均值,样本标准差是样本数据的离散程度的度量。
3. 确定Z值或t值:Z值和t值是根据置信水平和样本分布确定的。对于正态分布的总体,可以使用Z值;对于非正态分布的总体或样本量较小时,可以使用t值。Z值和t值可以从标准正态分布表或t分布表中查找。
4. 计算标准误差:标准误差是样本标准差除以样本大小的平方根(即标准差/√n)。标准误差反映了样本均值与总体均值之间可能存在的误差。
5. 代入公式计算置信区间:对于正态分布的总体,置信区间的计算公式为:置信区间 = 样本均值 ± Z值 × 标准误差。对于非正态分布的总体或样本量较小时,可以使用t分布来计算置信区间,此时公式为:置信区间 = 样本均值 ± t值 × 标准误差/√n。
置信区间的影响因素
置信区间的宽度受到多个因素的影响,主要包括样本量、置信水平和数据的变异性。
1. 样本量:在置信水平固定的情况下,样本量越多,置信区间越窄。这是因为随着样本量的增加,样本均值与总体均值之间的误差会逐渐减小,从而导致置信区间变窄。然而,置信区间变窄的速度并不像样本量增加的速度那么快。实践证明,样本量要增加4倍,置信区间才能变窄一半。
2. 置信水平:在样本量相同的情况下,置信水平越高,置信区间越宽。这是因为较高的置信水平意味着我们需要更多的范围来包含总体参数的真实值,从而导致置信区间变宽。
3. 数据的变异性:数据的变异性也会影响置信区间的宽度。如果数据变异性较大,即样本标准差较大,那么置信区间会相应变宽。反之,如果数据变异性较小,置信区间会相应变窄。
置信区间的实际应用
置信区间在统计学和实际应用中具有广泛的应用,包括参数估计、假设检验、质量控制、市场调研等。
1. 参数估计:置信区间可以用于估计总体参数的值。例如,在市场调研中,我们可以通过对一部分消费者进行调查,然后利用置信区间来估计整体消费者的偏好或满意度。
2. 假设检验:置信区间可以用于进行假设检验。例如,在医学研究中,我们可以利用置信区间来判断某种药物的疗效是否显著。如果置信区间不包含零值,则我们可以认为药物的疗效是显著的。
3. 质量控制:置信区间可以用于质量控制。例如,在生产过程中,我们可以通过对一部分产品进行抽样检测,然后利用置信区间来估计整体产品的质量水平。如果置信区间落在可接受的质量范围内,则我们可以认为整体产品的质量是合格的。
4. 市场调研:置信区间在市场调研中具有重要作用。例如,在选举预测中,我们可以利用置信区间来估计候选人的支持率,并预测选举结果的可能性。
实例分析
为了更好地理解置信区间的计算方法,以下通过一个实例进行分析。
假设我们随机抽取了1000个美国人的样本,调查发现其中有63%的人喜欢足球。我们想知道这个比例是否能够代表整个美国人口的情况。为了计算置信区间,我们可以按照以下步骤进行:
1. 确定置信水平:选择95%的置信水平。
2. 收集样本数据:样本大小为1000,样本均值为63%,样本标准差为σ(这个值需要通过实际调查数据计算得出)。
3. 确定Z值
- 上一篇: 如何准确进行QQ账号价值评估?
- 下一篇: 打印机连接错误:检查打印机名称
-
 如何轻松计算置信区间?公式揭秘!资讯攻略11-07
如何轻松计算置信区间?公式揭秘!资讯攻略11-07 -
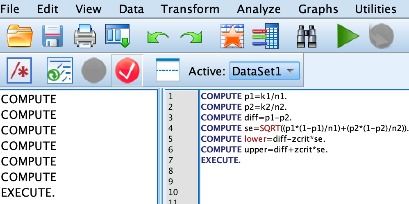 如何求总体率的95%可信区间?资讯攻略11-03
如何求总体率的95%可信区间?资讯攻略11-03 -
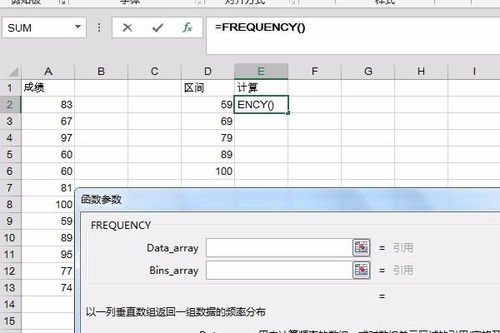 Excel高手必备:轻松掌握Frequency函数的使用方法!资讯攻略10-27
Excel高手必备:轻松掌握Frequency函数的使用方法!资讯攻略10-27 -
 起点的稿费制度是怎样的?500-10000订阅详细稿酬如何计算?资讯攻略11-12
起点的稿费制度是怎样的?500-10000订阅详细稿酬如何计算?资讯攻略11-12 -
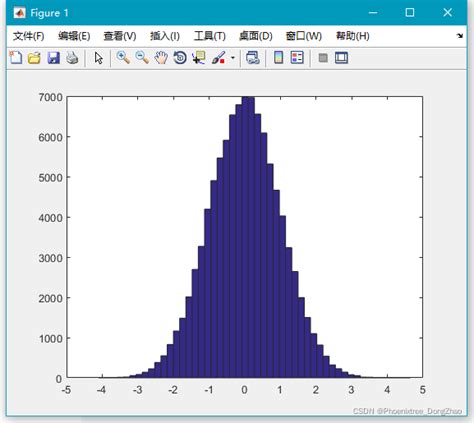 如何在MATLAB中轻松生成随机数资讯攻略12-09
如何在MATLAB中轻松生成随机数资讯攻略12-09 -
 裤子尺码S、M、L对应的腰围区间是多少?资讯攻略11-12
裤子尺码S、M、L对应的腰围区间是多少?资讯攻略11-12












