如何轻松计算置信区间?公式揭秘!
在统计学中,置信区间是一个非常重要的概念,它为我们提供了一种量化不确定性、评估参数估计值范围的方法。本文将详细介绍置信区间的计算公式,并通过合理的关键词布局、内容结构和语言表述,以提升阅读体验和搜索引擎友好度。

置信区间的基本概念
置信区间(Confidence Intervals),也被称为估计区间,是一个围绕某个参数估计值(如均值、比例等)的范围,该范围有特定的概率(即置信水平)包含真实的参数值。例如,一个95%的置信区间表示我们有95%的信心认为该区间包含了真实参数值。

置信区间的表达式通常写为:

\[
\text{Pr}(c1 \leq \mu \leq c2) = 1 - \alpha
\]
其中,$\mu$ 是我们感兴趣的参数(如总体均值),$c1$ 和 $c2$ 是区间的下限和上限,$\alpha$ 是显著性水平(如0.05),$1 - \alpha$ 是置信水平(如95%)。
置信区间的计算公式
总体均值的置信区间
对于总体均值的置信区间估计,我们常用的公式是:
\[
\bar{x} \pm z_{\frac{\alpha}{2}} \times \frac{\sigma}{\sqrt{n}}
\]
其中:
$\bar{x}$ 是样本均值。
$z_{\frac{\alpha}{2}}$ 是标准正态分布的分位数,对应于置信水平 $1 - \alpha$。例如,对于95%的置信水平,$z_{\frac{0.05}{2}} = 1.96$。
$\sigma$ 是总体标准差(如果未知,可用样本标准差 $s$ 替代,并使用 $t$ 分布计算相应的分位数)。
$n$ 是样本量。
样本比例或概率的置信区间
对于样本比例的置信区间估计,当样本量足够大时(如 $n \geq 30$),我们可以使用正态分布的近似方法,公式为:
\[
\hat{p} \pm z_{\frac{\alpha}{2}} \times \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}
\]
其中:
$\hat{p}$ 是样本比例。
$z_{\frac{\alpha}{2}}$ 同上。
$n$ 是样本量。
计算步骤
1. 确定置信水平:选择合适的置信水平,如95%或90%。
2. 查找分位数:根据置信水平和选择的分布(标准正态分布或 $t$ 分布),查找对应的分位数。
3. 计算标准误差:根据样本数据计算标准误差。
4. 构建置信区间:使用公式计算置信区间的下限和上限。
置信区间宽窄的影响因素
置信区间的宽度受以下因素影响:
1. 样本量:在其他因素不变的情况下,样本量越多,置信区间越窄。这是因为随着样本量的增加,样本均值的变异性减小,从而使估计更加精确。
2. 置信水平:在样本量相同的情况下,置信水平越高,置信区间越宽。高置信水平意味着我们希望区间更加保守,从而包含更多可能的真实值,导致区间宽度增加。
3. 总体标准差:总体标准差越大,置信区间越宽。这是因为总体标准差反映了数据的变异性,变异性越大,估计的不确定性也越大。
置信区间的实际应用
置信区间在统计学和实际问题中有着广泛的应用。例如:
市场调研:在调查消费者对某产品的满意度时,可以使用置信区间来估计真实满意度的范围。
医学研究:在评估某种药物的疗效时,可以使用置信区间来量化疗效的不确定性。
金融分析:在预测未来股价或市场走势时,可以使用置信区间来评估预测的准确性。
注意事项
1. 正确解读置信区间:置信区间是一个范围,而不是一个确定的值。我们不能说“参数等于某个置信区间的值”,而应该说“参数有95%的概率(或其他置信水平)落在该区间内”。
2. 选择合适的置信水平:置信水平的选择应根据具体问题的背景和要求来决定。一般来说,常用的置信水平有90%、95%和99%等。
3. 考虑样本的代表性和随机性:置信区间的有效性取决于样本的代表性和随机性。如果样本不具有代表性或存在偏差,则置信区间的估计结果可能不准确。
优化关键词布局和内容结构
为了提高文章的搜索引擎友好度和阅读体验,本文在撰写时进行了以下优化:
关键词布局:在文章中合理地使用了“置信区间”、“计算公式”、“置信水平”、“样本量”等关键词,并保持了适当的
- 上一篇: 如何在新浪微博上设置隐私,隐藏你的点赞记录?
- 下一篇: 如何用WinRAR制作自解压文件?
-
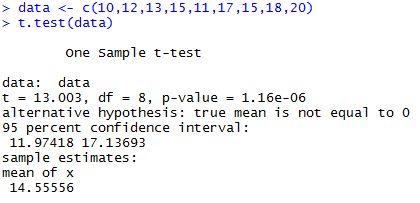 如何轻松计算置信区间?资讯攻略11-07
如何轻松计算置信区间?资讯攻略11-07 -
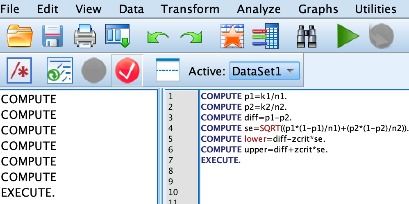 如何求总体率的95%可信区间?资讯攻略11-03
如何求总体率的95%可信区间?资讯攻略11-03 -
 揭秘等腰三角形边长计算的奥秘公式资讯攻略11-16
揭秘等腰三角形边长计算的奥秘公式资讯攻略11-16 -
 淘宝直通车推广:揭秘高效营销背后的核心计算公式资讯攻略11-24
淘宝直通车推广:揭秘高效营销背后的核心计算公式资讯攻略11-24 -
 揭秘积分基本公式:打开数学奥秘的大门资讯攻略12-09
揭秘积分基本公式:打开数学奥秘的大门资讯攻略12-09 -
 揭秘:灵敏度计算公式的奥秘与应用资讯攻略11-19
揭秘:灵敏度计算公式的奥秘与应用资讯攻略11-19












