揭秘积分基本公式:打开数学奥秘的大门
积分基本公式详解

在数学的广阔领域中,积分占据着举足轻重的地位。它不仅是连接微积分两大分支——微分与积分的桥梁,更是解决物理、工程、经济等众多实际问题不可或缺的工具。而积分基本公式,作为这一领域的基础,是每个有志于深入探索微积分奥秘的学习者必须掌握的知识点。

积分基本公式,通常指的是牛顿-莱布尼茨公式,也被称为微积分基本定理。这一公式揭示了定积分与不定积分之间的内在联系,为求解定积分提供了简便而有效的方法。具体而言,若函数f(x)在闭区间[a,b]上连续,F(x)是f(x)的一个原函数,则f(x)在[a,b]上的定积分等于F(b)与F(a)之差,即:
∫(a,b)f(x)dx = F(b) - F(a)
这个公式的重要性不言而喻,它使得我们不必再局限于繁琐的几何方法或数值逼近,而是可以通过求解不定积分来快速得到定积分的值。
然而,要熟练运用牛顿-莱布尼茨公式求解定积分,我们首先需要掌握一些基本的不定积分公式,即所谓的“积分基本公式表”。这些公式包括了幂函数、指数函数、对数函数、三角函数以及它们的复合函数等常见函数的积分形式。以下是一些基本的积分公式:
1. 幂函数积分公式:
∫x^ndx = (1/(n+1))x^(n+1) + C (n ≠ -1)
特别地,当n=-1时,有:
∫(1/x)dx = ln|x| + C
2. 指数函数积分公式:
∫a^xdx = (a^x/ln a) + C (a > 0, a ≠ 1)
3. 对数函数积分公式:
∫ln x dx = x ln x - x + C
4. 三角函数积分公式:
∫sin x dx = -cos x + C
∫cos x dx = sin x + C
∫tan x dx = -ln|cos x| + C
∫cot x dx = ln|sin x| + C
∫sec^2 x dx = tan x + C
∫csc^2 x dx = -cot x + C
∫sec x tan x dx = sec x + C
∫csc x cot x dx = -csc x + C
5. 反三角函数积分公式:
∫(1/√(1-x^2))dx = arcsin x + C
∫(1/(1+x^2))dx = arctan x + C
∫(1/|x|√(x^2-1))dx = arcsec x + C 或 arccsc x + C (根据x的符号选择)
掌握这些基本公式后,我们就可以通过凑微分、换元法、分部积分法等技巧来求解更复杂的积分问题。例如,对于形如∫e^(ax)sin(bx)dx的积分,我们可以先通过凑微分将其转化为已知公式的形式,或者利用分部积分法进行求解。
此外,积分基本公式在解决实际问题时也发挥着重要作用。比如,在物理学中,定积分常被用来求解物体的位移、速度、加速度等物理量;在工程学中,它可以用来计算面积、体积、质量分布等;在经济学中,定积分则可用于计算总收入、总成本等经济指标。
值得注意的是,虽然积分基本公式为我们提供了求解积分的强大工具,但在实际应用中仍需谨慎。因为积分的结果往往与函数的定义域、奇偶性、周期性等性质密切相关,稍有不慎就可能导致错误的结果。因此,在求解积分时,我们不仅要熟练掌握基本公式和求解技巧,还要对函数的性质有深入的理解。
此外,随着计算机技术的飞速发展,各种数学软件和编程语言都提供了强大的积分求解功能。这些工具不仅可以快速准确地求解复杂的积分问题,还可以帮助我们验证手算结果的正确性。因此,在学习积分基本公式的同时,我们也应该学会利用现代技术手段来提高自己的计算效率和准确性。
综上所述,积分基本公式是微积分学中的核心内容之一,它为我们提供了求解定积分和不定积分的有效方法。通过熟练掌握这些公式和相关的求解技巧,我们可以更好地理解和应用微积分知识,为解决实际问题提供有力的数学支持。同时,我们也应该不断学习和探索新的数学工具和方法,以适应时代发展的需要和个人成长的追求。
- 上一篇: DNF双开游戏秘籍:轻松实现双开攻略
- 下一篇: 轻松步骤:如何快速申请你的微信帐号
-
 揭秘立方根公式的奥秘!资讯攻略12-01
揭秘立方根公式的奥秘!资讯攻略12-01 -
 揭秘卷积运算:深度学习与图像处理背后的神奇公式资讯攻略10-26
揭秘卷积运算:深度学习与图像处理背后的神奇公式资讯攻略10-26 -
 负数减正数的结果是什么,有公式吗?资讯攻略01-08
负数减正数的结果是什么,有公式吗?资讯攻略01-08 -
 揭秘:灵敏度计算公式的奥秘与应用资讯攻略11-19
揭秘:灵敏度计算公式的奥秘与应用资讯攻略11-19 -
 揭秘:椭圆周长公式的神奇奥秘资讯攻略11-12
揭秘:椭圆周长公式的神奇奥秘资讯攻略11-12 -
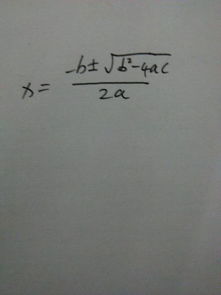 揭秘:掌握解方程的六大关键公式!资讯攻略11-09
揭秘:掌握解方程的六大关键公式!资讯攻略11-09