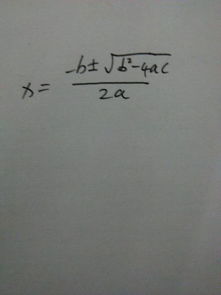已知方程x²+mx-2=0的一个解是x=2，求m的值

在数学领域中，方程求解是一项基础而重要的技能。它不仅能够帮助我们理解数学中的数量关系，还能广泛应用于物理、工程、经济等多个领域。今天，我们将通过一个具体的例子——已知关于x的方程x²+mx-2=0的一个解为x=2，来探讨如何求解方程中的未知数m，并借此机会深入理解二次方程的性质和解法。

首先，让我们明确题目给出的条件：我们有一个二次方程x²+mx-2=0，并且知道这个方程的一个解是x=2。我们的目标是求出未知数m的值。

为了求解m，我们需要利用二次方程的一个重要性质：一个二次方程如果有解，那么这些解应该能够使方程左右两边相等。换句话说，我们可以将已知的解代入方程，从而得到一个关于未知数的等式，进而求解未知数。

现在，我们将x=2代入方程x²+mx-2=0中。代入后，我们得到：

2²+2m-2=0

化简后，我们得到一个关于m的一元一次方程：

4+2m-2=0

进一步化简，得到：

2m+2=0

解这个一元一次方程，我们得到：

m=-1

因此，我们找到了未知数m的值，即m=-1。这个求解过程充分利用了二次方程解的性质，通过代入法求解了未知数。

在求解过程中，我们还需要注意一些细节。首先，要确保代入法的正确性，即将已知的解准确地代入方程中。其次，在化简方程时，要注意运算的准确性和步骤的清晰性，以避免出现错误。最后，在求解未知数时，要仔细检查解的正确性，确保解满足原方程。

此外，这个求解过程也体现了数学中的抽象思维和逻辑推理能力。我们需要从具体的数学问题中抽象出数学模型，然后通过逻辑推理和数学运算求解未知数。这种能力不仅在数学学习中至关重要，也是我们在日常生活和工作中解决问题的重要工具。

接下来，我们进一步探讨这个二次方程x²+mx-2=0的其他性质。由于我们已经找到了一个解x=2和对应的m值m=-1，我们可以将m值代入原方程，得到完整的二次方程：

x²-x-2=0

这个方程是一个标准的二次方程，具有二次方程的一般性质。例如，我们可以利用求根公式求解这个方程的另一个解。求根公式是二次方程求解的一种通用方法，它适用于所有形式为ax²+bx+c=0的二次方程。

对于方程x²-x-2=0，我们可以将其看作a=1，b=-1，c=-2。将这些值代入求根公式中，我们可以得到方程的两个解。由于我们已经知道其中一个解是x=2，所以我们可以通过求根公式验证这个解的正确性，并求出另一个解。

经过计算，我们发现求根公式给出的两个解确实是x=2和另一个我们尚未求出的解（通过计算可得另一个解为x=-1）。这进一步验证了我们的求解过程和结果的正确性。

此外，我们还可以利用二次方程的判别式来判断方程的解的情况。判别式Δ=b²-4ac是一个重要的数学工具，它可以告诉我们二次方程的解是实数还是复数，以及方程是否有重根。

对于方程x²-x-2=0，我们可以计算判别式Δ=(-1)²-4×1×(-2)=9。由于Δ>0，我们知道这个方程有两个不相等的实数解。这再次验证了我们的求解过程和结果的正确性。

最后，我们回顾一下这个求解过程的整体思路。我们从题目给出的条件出发，利用二次方程解的性质和代入法求解了未知数m。然后，我们验证了求解过程的正确性和结果的准确性，并探讨了二次方程的其他性质。这个求解过程不仅锻炼了我们的数学运算能力和逻辑推理能力，还让我们更加深入地理解了二次方程的性质和解法。

通过这个例子，我们可以看到数学中的每一个知识点都不是孤立的，它们之间有着紧密的联系和相互的支撑。在学习数学时，我们应该注重知识的系统性和整体性，将各个知识点串联起来形成一个完整的知识体系。这样，我们才能更好地理解和应用数学知识，提高我们的数学素养和解决问题的能力。

同时，我们也应该注重数学实践和应用。数学不仅仅是一门理论学科，它更是一门实践学科。通过解决实际问题，我们可以将数学知识转化为实际技能，提高我们的实践能力和创新能力。因此，在学习数学时，我们应该多做一些实际应用的题目和练习，将数学知识与实际问题相结合，培养我们的数学应用能力和解决问题的能力。

总之，通过求解这个关于x的二次方程x²+mx-2=0的未知数m的过程，我们不仅锻炼了数学运算能力和逻辑推理能力，还深入理解了二次方程的性质和解法。同时，我们也看到了数学中的知识点之间的相互联系和支撑以及数学实践和应用的重要性。希望这个例子能够激发你对数学的兴趣和热情，让你更加喜欢数学并愿意在数学领域不断探索和前行。