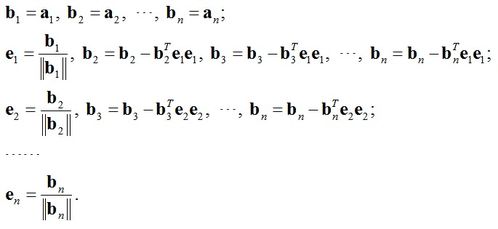揭秘正交矩阵:定义与特性全解析
正交矩阵是线性代数中一个非常关键且有趣的概念。在数学、物理学以及工程学等领域中,正交矩阵都扮演着极其重要的角色。为了全面理解正交矩阵,我们需要从其定义、性质、判别方法以及应用等多个方面进行探讨。

首先,正交矩阵的定义涉及到一个核心概念——正交性。在欧几里得空间中,如果两个向量的点积为零,则称这两个向量是正交的。推广到矩阵层面,如果一个矩阵的转置矩阵等于其逆矩阵,则称这个矩阵为正交矩阵。换句话说,如果矩阵A满足条件A的转置乘A等于单位矩阵I(即AT*A=I),则A就是正交矩阵。这里,AT表示A的转置矩阵,I是单位矩阵。

正交矩阵具有许多独特的性质,这些性质使得正交矩阵在实际应用中具有极大的优势。首先,正交矩阵的乘积仍然是正交矩阵。这意味着,如果我们有两个正交矩阵A和B,那么它们的乘积AB也是正交矩阵。这一性质为我们在构建复杂变换时提供了极大的便利。

其次,正交矩阵的行列式值为1或-1。这是因为正交矩阵的转置矩阵等于其逆矩阵,所以行列式值满足det(A)=det(AT)=1/det(A)。从这个等式我们可以推导出,det(A)的平方等于1,因此det(A)只能是1或-1。这一性质揭示了正交矩阵在体积变换方面的特性:正交矩阵不会改变空间体积的大小,只会改变空间的方向和形状。
再者,正交矩阵的特征值只能是1或-1。这是由正交矩阵的性质决定的。正交矩阵在变换空间中保持向量的长度不变(即模长保持不变),因此其特征值只能是1(表示向量方向不变)或-1(表示向量方向反向)。这一性质在图像处理、信号处理等领域有着广泛的应用。
正交矩阵的判别方法相对简单。最直接的方法是检查矩阵的转置矩阵是否等于其逆矩阵。但这种方法计算量较大,尤其在矩阵规模较大时不太实用。另一种更实用的方法是利用正交矩阵的性质进行判别。例如,我们可以检查矩阵的行向量或列向量是否两两正交且模长为1。如果满足这些条件,则矩阵就是正交矩阵。
此外,正交矩阵还可以通过一些特殊的生成方法来构建。例如,利用Gram-Schmidt正交化过程,我们可以将一组线性无关的向量转化为正交向量组,从而构建出正交矩阵。另外,一些特殊的矩阵(如置换矩阵、旋转矩阵等)也是正交矩阵的特例。
正交矩阵在诸多领域中都有着广泛的应用。在几何学中,正交矩阵可以用来描述旋转、反射等变换。这些变换在图形学、计算机视觉等领域中具有重要意义。例如,在计算机图形学中,我们可以使用正交矩阵来实现物体的旋转、缩放和投影等操作。这些操作对于创建逼真的三维场景和动画至关重要。
在物理学中,正交矩阵也有着广泛的应用。例如,在量子力学中,波函数的变换通常需要用到正交矩阵。这是因为正交矩阵能够保持波函数的模长不变,从而确保物理量的守恒。此外,在量子力学中还存在一种特殊的正交矩阵——幺正矩阵,它描述了量子态之间的变换关系。
在信号处理和通信领域,正交矩阵同样发挥着重要作用。例如,在正交频分复用(OFDM)技术中,正交矩阵被用来将信号分割成多个并行的子载波,从而实现高速数据传输。此外,在信号处理中,正交矩阵还可以用来进行滤波、去噪和特征提取等操作。
在数据分析和机器学习领域,正交矩阵也有着广泛的应用。例如,在主成分分析(PCA)中,我们利用正交矩阵将原始数据投影到一个低维空间中,从而提取出数据的主要特征。这种方法在数据降维、特征提取和图像压缩等领域中具有广泛的应用价值。
此外,正交矩阵还在密码学、统计学和经济学等领域中发挥着重要作用。在密码学中,正交矩阵可以用来构建安全的加密算法;在统计学中,正交矩阵可以用来进行方差分析和回归分析等操作;在经济学中,正交矩阵则可以用来描述不同经济变量之间的关系和变动规律。
综上所述,正交矩阵是一个具有广泛应用和深入研究价值的数学概念。它不仅在数学领域中扮演着重要角色,还在物理学、工程学、信号处理、数据分析和机器学习等多个领域中发挥着重要作用。因此,深入理解正交矩阵的定义、性质、判别方法以及应用对于提高我们的数学素养和解决实际问题具有重要意义。
通过对正交矩阵的全面探讨,我们可以发现正交矩阵在数学和实际应用中具有许多独特的优势和价值。它不仅能够帮助我们更好地理解和描述空间变换和物理现象,还能够为我们提供有效的数据分析和机器学习方法。因此,在学习和研究过程中,我们应该注重理解和掌握正交矩阵的相关知识和技能,以便更好地应用它们来解决实际问题。
- 上一篇: 揭秘泛性恋:含义与解析
- 下一篇: 探索“骸”字的正确发音,揭秘其独特韵味
-
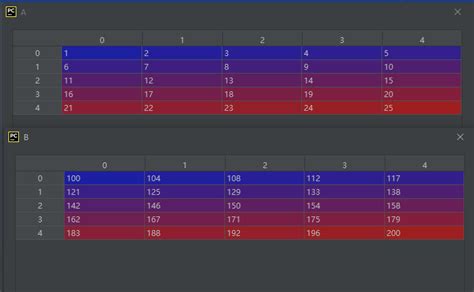 什么是OpenCV中的norm函数?范数求解全解析资讯攻略11-04
什么是OpenCV中的norm函数?范数求解全解析资讯攻略11-04 -
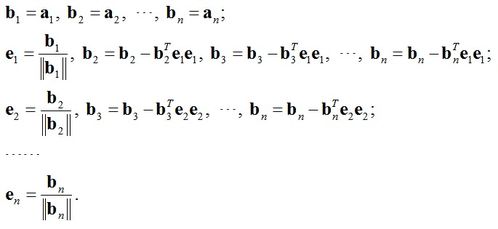 施密特正交化方法的定义是什么?资讯攻略02-18
施密特正交化方法的定义是什么?资讯攻略02-18 -
 揭秘套房:定义与特色全解析资讯攻略01-15
揭秘套房:定义与特色全解析资讯攻略01-15 -
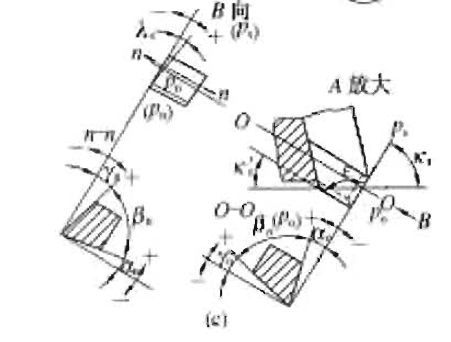 揭秘车刀角度的精准定义与奥秘资讯攻略12-04
揭秘车刀角度的精准定义与奥秘资讯攻略12-04 -
 揭秘职场多彩领域:蓝领、白领、粉领、钻石领定义及差异全解析资讯攻略12-07
揭秘职场多彩领域:蓝领、白领、粉领、钻石领定义及差异全解析资讯攻略12-07 -
 揭秘图种:定义与打开方法全解析资讯攻略10-30
揭秘图种:定义与打开方法全解析资讯攻略10-30