cotx的等效公式是什么?
cotx等于什么公式
cotx,即余切函数,是三角函数中的一种,全称为cotangent。在数学、物理、工程等领域,cotx函数都有着广泛的应用。在本文中,我们将从定义、运算关系、性质及应用等多个维度来深入探讨cotx的公式及其相关知识。

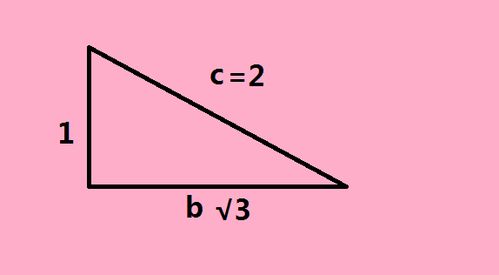
首先,cotx的定义可以从几何和代数两个角度进行阐述。在直角三角形的背景下,cotx等于相邻直角边与对边长度的比值,即cotx = 邻边/对边。从代数角度看,cotx是cosx与sinx的商,也就是cotx = cosx/sinx。此外,cotx还可以表示为cotx = 1/tanx,即cotx是正切函数的倒数。

接下来,我们讨论cotx的运算关系。三角函数之间具有紧密的联系和运算关系,cotx也不例外。这些关系包括平方关系、倒数关系和商的关系。平方关系指的是(sinx)^2 + (cosx)^2 = 1,由此可以推导出1 + (tanx)^2 = (secx)^2 和 1 + (cotx)^2 = (cscx)^2。倒数关系表明sinx与cscx互为倒数,cosx与secx互为倒数,tanx与cotx互为倒数。商的关系则体现在sinx/cosx = tanx,tanx/secx = sinx,cotx/cscx = cosx等表达式中。

cotx函数具有一些重要的性质,这些性质包括定义域、周期性、奇偶性和单调性等。由于分母sinx不能为0,cotx的定义域为{x | x ≠ kπ, k ∈ Z},即所有不等于kπ(k为整数)的实数。cotx是一个周期函数,其周期为π。这意味着对于任意的整数k,cot(x + kπ) = cotx。cotx还是一个奇函数,满足cot(-x) = -cotx。当x = nπ(n为整数)时,sinx = 0,此时cotx无定义。在一个周期内,cotx函数在某些区间上单调递减,在某些区间上单调递增。
cotx函数在实际问题中的应用非常广泛。在解决与三角形相关的问题时,cotx函数特别有用,特别是当需要找出与给定角度对应的边长比例时。例如,在直角三角形中,如果我们知道一个角度和一条边的长度,就可以利用cotx函数求出另一条边的长度。在物理学中,cotx函数可以用于描述振荡运动。在工程学中,cotx函数则常用于计算建筑物的稳定性,通过测量建筑物的倾斜角度并利用cotx函数进行计算,可以评估建筑物的稳定性。在计算机科学中,cotx函数也应用于计算机图形学中的三角形变换问题和机械工程中的运动学问题等。
cotx函数与其他三角函数之间具有紧密的联系和相互转换的关系。例如,tanx和cotx可以用tanx = 1/cotx相互转换。sinx和cosx与cotx的关系体现在cotx = cosx/sinx这一公式中。此外,sinx和cosx也可以用sinx = 1/cscx和cosx = 1/secx与cscx和secx相互转换。这些转换关系为三角函数在实际问题中的应用提供了极大的便利。
在深入学习cotx函数的过程中,我们还需要注意一些常见的误区和错误。例如,在计算cotx时,需要注意sinx不能为0,否则cotx将无定义。此外,在应用cotx函数解决实际问题时,需要根据问题的具体背景和要求,选择合适的三角函数及其关系式进行计算。
为了更好地理解和应用cotx函数,我们可以通过一些具体的例子来加以说明。例如,求45度的余切值。在45度的直角三角形中,邻边和对边的长度相等,所以cot(45°) = 1/1 = 1。再例如,求在x = π处cotx的值。由于当x = π时,sinπ = 0,导致cotπ无定义。这些例子不仅有助于我们加深对cotx函数的理解,还能提高我们应用cotx函数解决实际问题的能力。
cotx函数在三角函数的学习中占据着重要的地位。它与正弦函数sinx、余弦函数cosx、正切函数tanx等共同构成了三角函数的基本体系。这些函数之间有着密切的联系和相互转换的关系,如cotx = 1/tanx,tanx = sinx/cosx等。掌握这些函数的基本性质和转换关系对于深入理解三角函数以及应用它们解决实际问题具有重要意义。
此外,cotx函数的学习还可以帮助我们培养逻辑思维和抽象思维能力。在学习cotx函数的过程中,我们需要运用逻辑思维来分析和解决问题,需要运用抽象思维能力来理解和掌握cotx函数的定义、性质和应用。这些思维能力的培养不仅有助于我们学好三角函数,还能对我们的学习和生活产生积极的影响。
综上所述,cotx等于cosx/sinx或1/tanx,是三角函数中的一个重要概念。它在数学、物理、工程和计算机科学等领域中都有着广泛的应用。在学习cotx函数的过程中,我们需要掌握其定义、运算关系、性质及应用等方面的知识,并注意避免常见的误区和错误。通过不断学习和实践,我们可以更好地理解和掌握cotx函数,提高我们的数学素养和解决实际问题的能力。
- 上一篇: 解析'四面八方'的含义
- 下一篇: 侨字可以组成哪些词?
-
 cotx的等价公式是什么?资讯攻略02-05
cotx的等价公式是什么?资讯攻略02-05 -
 频率的计算公式是什么资讯攻略11-13
频率的计算公式是什么资讯攻略11-13 -
 揭秘:泊松分布公式的奥秘是什么?资讯攻略04-07
揭秘:泊松分布公式的奥秘是什么?资讯攻略04-07 -
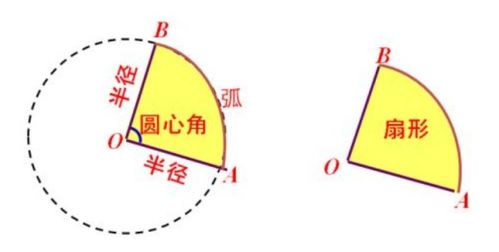 扇形面积计算的三大公式是什么?资讯攻略10-25
扇形面积计算的三大公式是什么?资讯攻略10-25 -
 负数减正数的结果是什么,有公式吗?资讯攻略01-08
负数减正数的结果是什么,有公式吗?资讯攻略01-08 -
 资深解析:银行存款偏离度计算公式是什么?怎么运用?资讯攻略12-05
资深解析:银行存款偏离度计算公式是什么?怎么运用?资讯攻略12-05