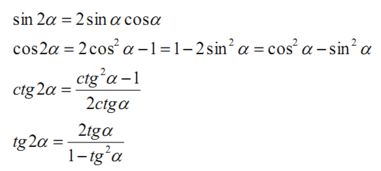揭秘:泊松分布公式的奥秘是什么?
泊松分布公式是什么?

泊松分布(Poisson distribution),又称波哇松分布、卜瓦松分布,是一种重要的离散型概率分布,广泛应用于描述固定时间或空间内某稀有事件发生次数的概率分布。它首次由法国数学家西莫恩·德尼·泊松在1837年提出,自那时起,泊松分布在概率统计和数据分析中占据了重要位置。本文将详细介绍泊松分布的公式、参数含义、基本性质、适用条件及实际应用等多个维度,帮助读者全面理解这一重要的统计工具。

一、泊松分布公式及其组成
泊松分布的公式为P(X=k) = (λ^k * e^(-λ)) / k!,其中X代表事件发生次数,k为具体发生次数,λ为事件平均发生率,e为自然对数的底数。公式的核心由四部分构成:
1. λ^k:表示事件平均发生率λ的k次方。λ需为正实数(λ>0),代表单位时间或空间内事件的平均发生次数。
2. e^(-λ):自然对数的底数e的负λ次方,用于调整概率随λ变化的衰减幅度。
3. k!:k的阶乘,即k×(k-1)×…×1,用于归一化概率值,使得所有可能事件发生的概率之和为1。
4. P(X=k):表示在单位时间内事件恰好发生k次的概率。
二、参数λ的作用
在泊松分布中,λ是唯一的参数,它决定了分布的形状和特征:
1. 数学性质:λ既是分布的均值E(X),也是方差Var(X),即E(X)=Var(X)=λ。这一性质使得泊松分布在数学处理上更为简便。
2. 实际意义:λ代表单位时间或空间内事件的平均发生次数。例如,若某医院每小时平均接收3名急诊患者(λ=3),则λ=3表示每小时的平均接诊量。
3. 分布形态:λ较小时,概率分布右偏;λ增大时,分布逐渐对称并接近正态分布。当λ较大(通常λ>10)时,泊松分布近似服从正态分布N(λ, λ)。
三、泊松分布的基本性质
1. 离散型分布:泊松分布描述的是离散型随机变量,其取值只能是非负整数(如0,1,2,…),表示事件发生的次数。
2. 期望与方差相等:泊松分布的期望值(均值)和方差均为参数λ,这是其区别于其他分布的重要特征。
3. 趋近正态分布:当λ较大时,泊松分布近似服从正态分布。这一性质使得在大样本情况下,泊松分布的计算和分析更为简便。
4. 可加性:若多个独立的泊松分布随机变量相加(如X~Poi(λ₁), Y~Poi(λ₂)),则X+Y服从Poi(λ₁+λ₂)。这一性质使得泊松分布在处理多个独立事件时具有极大的灵活性。
5. 稀有事件性质:泊松分布通常用于描述单位时间或空间内稀有事件(低概率事件)的发生次数,如电话呼叫次数、缺陷产品数等。这一性质使得泊松分布在处理稀有事件时具有独特的优势。
四、泊松分布的适用条件
泊松分布在实际应用中需要满足以下条件:
1. 事件独立性:任意两个时间段内事件发生相互独立。即一个事件的发生不会影响另一个事件的发生。
2. 发生率恒定:单位时间(或空间)内事件的平均发生率稳定不变。即λ在整个研究期间内保持不变。
3. 低概率性:短时间内发生两次及以上事件的概率趋近于0。这一条件保证了泊松分布在描述稀有事件时的准确性。
五、泊松分布的实际应用
泊松分布在多个领域中得到了广泛应用,尤其是在研究随机、独立事件发生频率的情境下。以下是一些典型的应用领域:
1. 电话交换与通信网络:在电话交换系统中,电话呼入的频率可以被视为一个随机过程。假设某个时间段内电话呼入的平均次数为λ,那么在这一时间段内,电话呼入k次的概率就遵循泊松分布。类似的,互联网流量、数据包的传输等也常常可以通过泊松分布来建模和分析。
2. 生产质量控制:在生产线质量控制中,若某条生产线在单位时间内的平均故障次数为λ,则故障发生的次数服从泊松分布。通过分析泊松分布,可以有效地进行质量控制、预测维修时间和优化生产流程。
3. 计算机科学与系统工程:在计算机系统中,故障的发生、程序错误、服务器请求等也常常符合泊松分布。例如,在某个时间窗口内服务器请求的数量,若请求是随机到达的,则可通过泊松分布来预测系统负载和处理能力。
4. 天文物理与粒子物理:在粒子物理学和天文观测中,泊松分布常用于描述粒子或天体事件的出现。例如,某一单位时间内的光子到达次数、某种粒子探测器接收到的信号次数等,这些现象均可通过泊松分布进行建模和分析。
此外,泊松分布还应用于放射性物质衰变次数、客服中心每分钟接到的电话数、汽车站台的候客人数、机器出现的故障数、DNA序列的变异数等多个领域。这些应用充分展示了泊松分布在描述随机事件发生频次方面的强大能力。
六、结论
泊松分布作为一种强大的概率模型,在多个领域中都有着广泛的应用。其简洁的数学形式将事件的平均发生率与具体发生次数的概率关联起来,使得在数据分析中能够合理建模与决策。理解泊松分布的公式、参数含义、基本性质及适用条件,有助于读者更好地运用这一统计工具解决实际问题。同时,泊松分布的现实意义也揭示了其在描述随机事件发生频次方面的独特优势,使其成为许多实际问题分析的基础工具。
- 上一篇: 揭秘:“知名不具”究竟是何含义?
- 下一篇: 揭秘:与“right”发音相同的神秘词汇是什么?
-
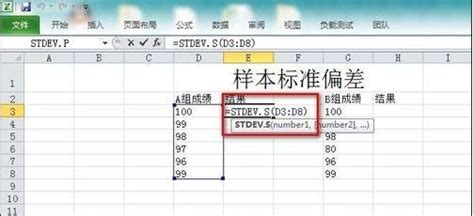 Excel中标准偏差的计算公式资讯攻略11-03
Excel中标准偏差的计算公式资讯攻略11-03 -
 揭秘积分基本公式:打开数学奥秘的大门资讯攻略12-09
揭秘积分基本公式:打开数学奥秘的大门资讯攻略12-09 -
 揭秘立方根公式的奥秘!资讯攻略12-01
揭秘立方根公式的奥秘!资讯攻略12-01 -
 揭秘等腰三角形边长计算的奥秘公式资讯攻略11-16
揭秘等腰三角形边长计算的奥秘公式资讯攻略11-16 -
 揭秘:灵敏度计算公式的奥秘与应用资讯攻略11-19
揭秘:灵敏度计算公式的奥秘与应用资讯攻略11-19 -
 揭秘:椭圆周长公式的神奇奥秘资讯攻略11-12
揭秘:椭圆周长公式的神奇奥秘资讯攻略11-12