探索平方根公式的奥秘
平方根公式是数学中一个极为基础且重要的概念,它不仅能够帮助我们求解一个数的平方根,还在代数、几何、物理等多个学科领域中发挥着不可替代的作用。本文将详细介绍平方根公式的定义、推导、应用以及与之相关的一些重要性质,旨在帮助那些对平方根公式感兴趣的朋友全面而深入地理解这一概念。
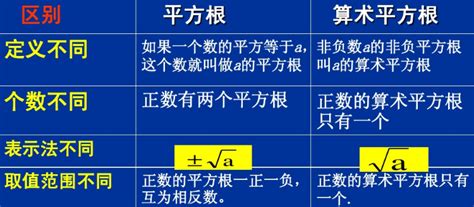
首先,我们需要明确什么是平方根。平方根是一个数,它乘以自己(即自乘)的结果等于原数。例如,数字4的平方根是2,因为2乘以2等于4。同样,数字9的平方根是3或-3,因为3乘以3等于9,且-3乘以-3也等于9。在这里,我们特别关注的是非负实数的平方根,即算术平方根,它总是非负的。
平方根公式通常指的是求解一个非负实数平方根的表达式。在实数范围内,对于任意非负实数a(a≥0),其平方根可以表示为√a,读作“根号a”。这个符号“√”被称为根号,它表示对括号内的数进行开方运算。
接下来,我们探讨平方根公式的推导。虽然平方根的概念相对直观,但其背后的数学原理却值得深入探讨。平方根公式的推导可以从平方运算的逆运算角度入手。平方运算是指一个数乘以自己,而平方根运算则是平方运算的逆运算,即找到一个数,使其平方等于原数。
为了求解一个数的平方根,我们可以采用逼近法。例如,对于给定的非负实数a,我们可以设置一个初始值x0,然后不断迭代计算x(n+1)=(x(n)+a/x(n))/2,直到x(n+1)与x(n)的差值小于一个预定的精度值。这种方法被称为牛顿迭代法,它能够快速而准确地逼近平方根的真实值。
然而,在实际应用中,我们更常用的是平方根的直接计算公式,即利用计算器或计算机中的平方根函数来求解。这些函数内部通常采用了更为复杂和高效的算法来确保计算的准确性和速度。
平方根公式在数学和实际应用中具有广泛的应用。在代数中,平方根公式是解方程的重要工具。例如,对于形如x^2=a的方程,我们可以直接利用平方根公式求解得到x=√a或x=-√a。在几何中,平方根公式与勾股定理紧密相连,它帮助我们求解直角三角形中的未知边长。在物理中,平方根公式也广泛应用于力、速度、加速度等物理量的计算中。
此外,平方根公式还与一些重要的数学常数和函数密切相关。例如,圆周率π和自然对数的底数e都与平方根运算有着千丝万缕的联系。在数学分析中,平方根函数f(x)=√x是一个典型的幂函数,它在定义域[0,+∞)上是单调递增的,并且具有连续性和可导性等重要性质。
值得注意的是,平方根公式在复数范围内同样适用。对于任意复数z=a+bi(a,b为实数),其平方根可以通过求解二次方程z^2=w得到。在复数范围内,平方根有两个解,它们互为共轭复数。这一性质使得平方根公式在复数分析和信号处理等领域中具有广泛的应用价值。
除了基本的平方根公式外,还有一些与平方根相关的公式和定理也值得我们关注。例如,平方差公式a^2-b^2=(a+b)(a-b)和完全平方公式(a+b)^2=a^2+2ab+b^2都涉及到了平方根的概念。这些公式和定理在代数运算和证明中发挥着重要的作用。
此外,还有一些与平方根相关的特殊性质也值得我们注意。例如,任何非零数的平方根的平方都等于原数本身;负数的平方根在实数范围内不存在,但在复数范围内有两个解;平方根函数在定义域上是连续的,但不可导于x=0点等。这些性质不仅丰富了平方根公式的内涵,也为我们更好地理解和应用平方根公式提供了有力的支持。
总的来说,平方根公式是数学中一个基础而重要的概念。它不仅能够帮助我们求解一个数的平方根,还在代数、几何、物理等多个学科领域中发挥着不可替代的作用。通过对平方根公式的深入理解和应用,我们可以更好地掌握数学的基本概念和方法,提高自己的数学素养和解决实际问题的能力。
对于那些对平方根公式感兴趣的朋友来说,建议你们进一步学习相关的数学知识和方法,如微积分、复变函数等,以便更深入地理解平方根公式的内涵和应用。同时,也可以尝试将平方根公式应用于实际问题中,通过实践来加深对其的理解和掌握。相信在不断的学习和实践中,你们一定能够取得更加丰硕的成果。
- 上一篇: 孤单的对立面是什么
- 下一篇: 一笔添变:个、古、亚、车、亿、灭,新字何现?
-
 揭秘立方根公式的奥秘!资讯攻略12-01
揭秘立方根公式的奥秘!资讯攻略12-01 -
 探索八平方米的空间奥秘资讯攻略02-25
探索八平方米的空间奥秘资讯攻略02-25 -
 探索1至30的数字奥秘:立方根一览表资讯攻略02-15
探索1至30的数字奥秘:立方根一览表资讯攻略02-15 -
 揭秘积分基本公式:打开数学奥秘的大门资讯攻略12-09
揭秘积分基本公式:打开数学奥秘的大门资讯攻略12-09 -
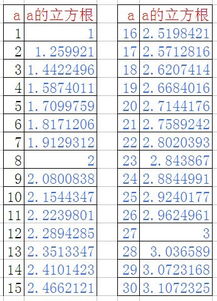 探索数学之美:1至30的数字立方根全览资讯攻略12-03
探索数学之美:1至30的数字立方根全览资讯攻略12-03 -
 揭秘:泊松分布公式的奥秘是什么?资讯攻略04-07
揭秘:泊松分布公式的奥秘是什么?资讯攻略04-07