立方体体积的计算公式是什么?
在我们日常生活中,无论是建筑、设计还是简单的几何学学习,立方体都是一个极为常见的几何形状。无论是孩子玩的积木,还是家中摆放的储物盒,甚至是宏伟的建筑外观,都可能蕴含着立方体的影子。而当我们谈论立方体时,一个无法回避的话题就是它的体积。那么,如何计算一个立方体的体积呢?这就不得不提到一个简单而强大的工具——立方体的体积公式。
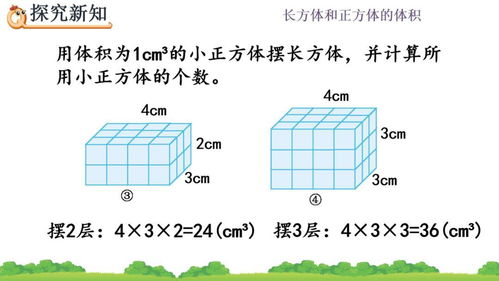
立方体的基本概念
首先,让我们来明确一下什么是立方体。立方体,顾名思义,是一个六个面都是正方形的立体图形。它的每一个角都是直角,每一条边都等长。这种简洁而对称的结构,使得立方体在自然界和人工制品中无处不在。

为什么需要计算立方体的体积?
计算立方体的体积,对于很多实际应用来说至关重要。比如,在建筑设计中,工程师需要知道一个立方体形状的房间能容纳多少空间,以确定其是否符合设计要求;在物流领域,包装设计师需要精确计算货物的体积,以确保它们能够高效地装载和运输;而在日常生活中,我们也可能需要估算一个储物盒能装下多少东西,这就需要用到立方体的体积计算。

立方体的体积公式
那么,如何计算立方体的体积呢?答案就藏在立方体的体积公式中:

立方体的体积 = 边长³
这个公式简单明了,却蕴含着强大的功能。它告诉我们,只需要知道立方体的任意一条边的长度,就可以轻松地计算出它的体积。
如何应用这个公式?
1. 确定边长:首先,你需要知道立方体的边长。这通常可以通过直接测量得到。比如,你有一个边长为5厘米的立方体盒子,那么它的边长就是5厘米。
2. 应用公式:接下来,将边长代入公式中进行计算。在这个例子中,体积 = 5厘米³ = 125立方厘米。
3. 理解结果:计算出的体积结果表示立方体内部的空间大小。在这个例子中,125立方厘米意味着这个盒子可以容纳125立方厘米的物体或空间。
公式背后的原理
虽然立方体的体积公式看起来很简单,但它背后蕴含着几何学的基本原理。想象一下,如果我们把一个立方体拆分成很多小的正方形(这些正方形是立方体的面),然后计算这些小正方形的面积并累加起来,我们实际上就得到了立方体的体积。但是,这种方法既繁琐又不直观。而立方体的体积公式则通过一种更为简洁和高效的方式,直接给出了体积的计算方法。
实际应用中的注意事项
在计算立方体的体积时,有几个实际应用中需要注意的事项:
单位统一:确保你使用的边长单位是统一的。比如,如果你用厘米作为单位测量边长,那么计算出的体积也将是立方厘米。如果你需要将其转换为其他单位(如立方米),则需要进行单位换算。
精度要求:在实际应用中,根据需求的精度不同,你可能需要对边长进行四舍五入或使用更高精度的测量工具。比如,在建筑设计中,可能需要精确到毫米甚至更小的单位来计算立方体的体积。
三维空间的理解:虽然立方体的体积公式很简单,但理解其背后的三维空间概念对于很多人来说可能是一个挑战。因此,在学习和应用这个公式时,不妨多结合一些实际的立方体模型或物体来帮助理解。
立方体的体积与表面积的关系
提到立方体的体积,不得不提一下它与表面积的关系。立方体的表面积公式是:
表面积 = 6 × 边长²
这个公式告诉我们,立方体的表面积与边长的平方成正比。与体积公式相比,表面积公式更多地反映了立方体外部的形态特征。而体积公式则关注的是立方体内部的空间大小。
在实际应用中,这两个公式往往需要结合使用。比如,在包装设计中,设计师不仅需要知道货物的体积以确保其能够装入包装盒中,还需要知道包装盒的表面积以确定需要多少包装材料。
立方体的体积公式在日常生活中的应用案例
家居设计:当你想要购买一个新的衣柜或书架时,你可能需要知道它的体积以确保它能够放入你的房间中。这时,你可以使用立方体的体积公式来计算衣柜或书架的体积。
厨房储物:在厨房里,你可能有很多不同大小的储物盒和罐子。为了更有效地利用空间,你可以使用立方体的体积公式来计算每个储物盒的体积,并根据需要调整它们的摆放位置。
园艺设计:在园艺设计中,你可能需要计算一个立方体形状的花盆或花坛的体积来确定需要多少土壤或肥料。这时,立方体的体积公式同样派得上用场。
结语
立方体的体积公式是一个简单而强大的工具,它能够帮助我们快速准确地计算出立方体的体积。无论是在建筑设计、物流规划还是日常生活中,这个公式都发挥着不可替代的作用。通过理解和掌握这个公式,我们可以更好地利用空间、规划物品和解决实际问题。因此,不妨在日常生活中多留意那些蕴含立方体形状的事物,并用立方体的体积公式去探索它们的内在奥秘吧!
- 上一篇: 手震:揭秘这一神秘现象的真正含义
- 下一篇: 如何评价北京冠领律师事务所?
-
 揭秘正方体体积的求解奥秘资讯攻略11-16
揭秘正方体体积的求解奥秘资讯攻略11-16 -
 立方体体积的计算方法资讯攻略10-30
立方体体积的计算方法资讯攻略10-30 -
 立方米与升之间如何快速换算?资讯攻略04-03
立方米与升之间如何快速换算?资讯攻略04-03 -
 工程力学中惯性矩的定义和计算公式是什么?资讯攻略02-13
工程力学中惯性矩的定义和计算公式是什么?资讯攻略02-13 -
 揭秘单位换算:如何将1升精准转换为吨?资讯攻略11-17
揭秘单位换算:如何将1升精准转换为吨?资讯攻略11-17 -
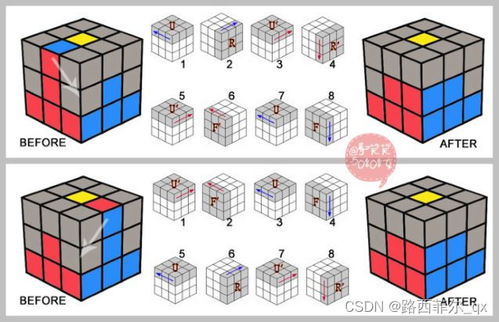 3x3魔方七步公式图解及口诀是什么?资讯攻略11-14
3x3魔方七步公式图解及口诀是什么?资讯攻略11-14