立方体体积的计算方法
在计算几何学中,计算一个立方体的体积是一个基本且重要的任务。立方体是一种特殊的多面体,其所有边都等长,且每个面都是一个正方形。要计算立方体的体积,我们需要了解它的一个基本属性:边长。通过边长,我们可以轻松计算出立方体的体积。下面将详细介绍如何计算立方体的体积,并在此过程中多次提及关键词,以提高文章的曝光率。

首先,我们需要明确立方体的定义。立方体是一种三维的几何形状,它有六个面,每个面都是一个正方形。由于立方体的所有边等长,我们只需要知道一个边的长度,就可以推导出整个立方体的体积。

计算立方体体积的公式是:体积 = 边长³。这个公式非常简洁,只需要将立方体的边长进行三次方运算,即可得到其体积。例如,如果一个立方体的边长是3厘米,那么它的体积就是3厘米³,或者写成数学表达式就是3³ = 27立方厘米。

在实际应用中,这个公式非常有用。比如,在建筑设计中,我们可能需要知道一个立方体房间的体积,以确定其能容纳多少空间。在物理实验中,我们也可能需要计算立方体容器的体积,以测量其中可以容纳多少液体或固体物质。
为了更深入地理解如何计算立方体的体积,我们可以通过一个具体的例子来说明。假设我们有一个边长为4厘米的立方体。首先,我们识别出这是一个立方体,并确定其边长。然后,我们将这个边长代入体积公式中进行计算。体积 = 边长³,所以体积 = 4厘米³ = 4³ = 64立方厘米。
此外,值得注意的是,立方体的体积与其边长是立方关系。这意味着,如果立方体的边长增加一倍,其体积将增加八倍。例如,如果一个立方体的边长是2厘米,其体积是2³ = 8立方厘米。而如果边长增加到4厘米(即增加一倍),体积则变为4³ = 64立方厘米,是原来的8倍。
在解决立方体体积问题时,我们还需要注意一些常见的误区。有些人可能会错误地认为立方体的体积是边长的平方再乘以一个常数。这是不正确的。立方体的体积是边长的三次方,而不是平方。因此,在计算时,一定要确保使用正确的公式。
此外,还有一些人可能会在计算过程中出错,比如忘记将边长进行三次方运算,或者在进行运算时出错。为了避免这些错误,建议在计算时仔细核对公式和运算步骤,确保每一步都正确无误。
另外,值得一提的是,立方体在几何学中有着特殊的地位。它是唯一一个所有边等长且每个面都是正方形的多面体。这种特性使得立方体在计算和构造上具有很多独特的性质和应用。例如,在三维空间中,立方体可以用来构建更复杂的几何形状,或者作为填充空间的基本单元。
在计算立方体体积的过程中,我们还可以将其与其他几何形状进行比较。比如,与长方体相比,立方体的计算更为简单,因为长方体的体积需要知道三个不同的边长(长、宽、高),而立方体只需要知道一个边长即可。然而,在实际应用中,长方体可能更为常见,因为很多实际物体并不是完全立方的。
除了立方体之外,还有其他一些几何形状也具有类似的体积计算公式。比如,球体的体积公式是(4/3)×π×半径³。虽然这个公式与立方体的体积公式不同,但它也涉及到了边长的三次方(在这里是半径的三次方)。这显示了三维空间中几何形状体积计算的一些共性。
此外,在计算立方体体积时,我们还可以将其与面积进行比较。立方体的表面积公式是6×边长²。虽然表面积和体积是两种不同的度量方式,但它们都涉及到立方体的边长。通过比较表面积和体积,我们可以更好地理解立方体在空间中的占据情况和性质。
总之,计算立方体的体积是一个简单而重要的任务。通过了解立方体的定义和性质,以及掌握正确的计算公式和运算步骤,我们可以轻松地计算出任何给定边长的立方体的体积。这个过程不仅可以帮助我们更好地理解几何学中的基本概念和原理,还可以在实际应用中发挥重要作用。
在计算过程中,我们需要注意公式的正确性和运算的准确性。同时,我们还可以通过比较立方体与其他几何形状的性质和应用,来更深入地理解几何学中的相关概念和原理。最终,通过不断学习和实践,我们可以不断提高自己的计算能力和对几何学的理解水平。无论是在学习、工作还是生活中,掌握如何计算立方体的体积都将是一项非常有用的技能。
- 上一篇: 如何开启百度账户管家的账号保护功能?
- 下一篇: 黄斑变性自查秘籍:如何用阿姆斯勒方格表进行自我检测?
-
 揭秘正方体体积的求解奥秘资讯攻略11-16
揭秘正方体体积的求解奥秘资讯攻略11-16 -
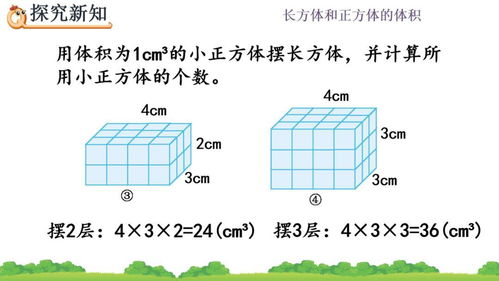 立方体体积的计算公式是什么?资讯攻略12-06
立方体体积的计算公式是什么?资讯攻略12-06 -
 立方米与升之间如何快速换算?资讯攻略04-03
立方米与升之间如何快速换算?资讯攻略04-03 -
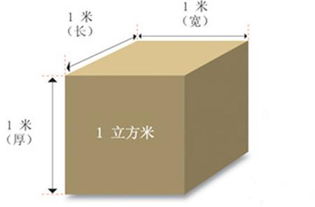 揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03
揭秘!1立方米竟然等于这么多立方厘米!资讯攻略12-03 -
 揭秘!1立方米究竟等于多少立方厘米?资讯攻略03-10
揭秘!1立方米究竟等于多少立方厘米?资讯攻略03-10 -
 一立方米砂的比重是多少?资讯攻略03-24
一立方米砂的比重是多少?资讯攻略03-24












