拐点：是点还是坐标的辨析

拐点是点还是坐标：一场关于几何与数学理解的探讨

在数学的浩瀚宇宙中，概念与定义如同星辰般繁多而璀璨，它们既是探索未知的灯塔，也是理解世界的钥匙。其中，“拐点”这一术语，在数学、物理学、工程学乃至经济学等多个领域都有着广泛的应用，但其本质意义却常常引发讨论与混淆。特别是关于“拐点是点还是坐标”的问题，更是让不少初学者感到困惑。本文旨在通过深入浅出的方式，解析拐点的本质，帮助读者全面理解这一概念。

一、拐点的初步认识

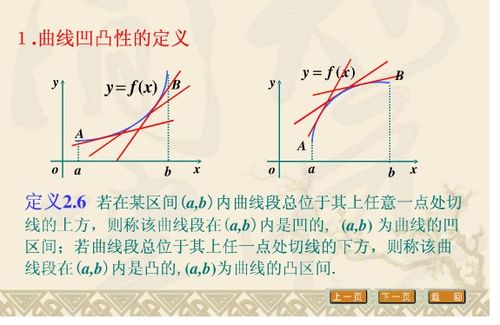
拐点，这一术语最初源自几何学，用于描述曲线上某一特殊位置的变化趋势。在直观上，我们可以将拐点想象为曲线上一个“弯曲方向发生改变”的点。例如，在一条先向上弯曲后向下弯曲的曲线上，那个由向上转为向下的点，即为拐点。从这一描述中，我们不难看出，拐点与曲线的形状密切相关，是曲线特征的一个重要标志。

二、拐点作为点的理解

在数学中，点是最基本的几何元素，它没有大小、形状、方向等属性，仅由位置确定。因此，当我们说拐点是点时，实际上是在强调其作为几何对象的基本属性。拐点作为曲线上的一个特殊点，其存在是由曲线本身的连续性、可导性等数学性质决定的。换句话说，拐点是曲线上满足一定条件（如二阶导数变号）的点。

三、拐点与坐标的关系

然而，仅仅将拐点视为一个抽象的点，并不能满足实际应用的需要。在解决实际问题时，我们通常需要知道拐点的具体位置，这就涉及到坐标的概念。在二维平面上，一个点的位置可以由其横坐标（x）和纵坐标（y）唯一确定。因此，拐点作为曲线上的一个具体点，自然也有其对应的坐标值。

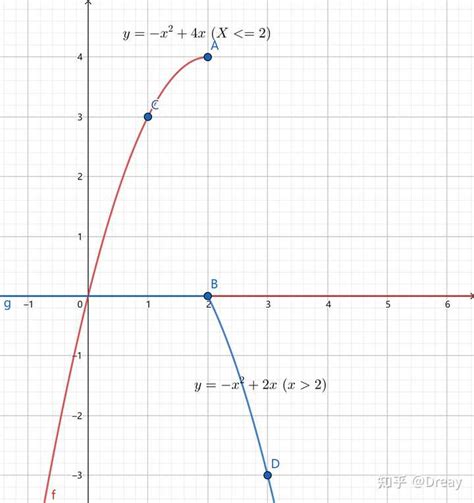
例如，在一条给定的函数曲线y=f(x)上，如果某点(x0, y0)满足f''(x0)=0且f'''(x0)≠0（其中f''(x)表示f(x)的二阶导数，f'''(x)表示f(x)的三阶导数），则该点即为拐点，其坐标即为(x0, y0)。这里，坐标不仅提供了拐点的具体位置信息，还成为了求解拐点的重要工具。

四、拐点概念的扩展与应用

随着数学的发展，拐点的概念逐渐被扩展到更广泛的领域。在物理学中，拐点常被用来描述物体运动轨迹的变化；在工程学中，拐点则是优化设计、分析结构稳定性的重要依据；在经济学中，拐点则象征着经济周期中增长趋势的转变。这些应用虽然各有特色，但都离不开对拐点本质的理解——即拐点作为曲线特征点的存在，以及通过坐标来确定其位置的方法。

五、拐点定义的深化与辨析

在深入探讨拐点概念时，我们还需要注意几个容易混淆的问题。首先，拐点与极值点不同。极值点是曲线上局部最大或最小的点，而拐点则是曲线上弯曲方向发生改变的点。其次，拐点并不总是伴随着极值点的存在。在某些情况下，拐点可能只是曲线形状的一个转折点，而不涉及任何极值。最后，拐点的存在条件在不同数学领域中可能有所不同。例如，在微积分中，拐点通常要求二阶导数变号；而在更一般的曲线论中，拐点的定义可能更加复杂，涉及更高阶的导数或曲率的变化。

六、拐点在解决实际问题中的应用案例

为了更好地理解拐点在实际问题中的应用，我们可以举几个具体的例子。在物理学中，研究物体运动轨迹时，拐点可以帮助我们预测物体运动方向的改变；在工程学中，分析梁的弯曲变形时，拐点则是确定梁上最大弯矩和剪力位置的关键；在经济学中，分析经济增长趋势时，拐点则预示着经济周期的转折点，对政策制定和投资决策具有重要指导意义。

七、拐点概念的哲学思考

拐点不仅是一个数学概念，它还蕴含着深刻的哲学意义。从哲学的角度看，拐点是事物发展过程中的一个关键时刻，它标志着旧阶段的结束和新阶段的开始。正如黑格尔所说：“每一个终点都是一个新的起点。”拐点正是这一哲学思想的生动体现。在人生的道路上，我们也需要学会识别并抓住那些关键的拐点，以实现个人的成长和突破。

八、结语

综上所述，拐点既是曲线上的一个特殊点，也是由该点坐标确定的具体位置。在数学的严格定义下，拐点作为曲线特征点的存在，通过坐标这一数学工具得以精确描述和定位。同时，拐点作为事物发展过程中的关键时刻，又蕴含着深刻的哲学意义。因此，当我们谈论拐点时，不应仅仅将其视为一个抽象的数学概念或具体的坐标值，而应将其视为一个连接数学、物理、工程、经济乃至人生哲学的桥梁。只有这样，我们才能更全面、更深刻地理解拐点这一概念，并将其应用于实际问题的解决中。