揭秘函数拐点:它们为何重要且如何识别?
在数学的广阔领域中,函数作为描述自然界和社会现象中数量关系的重要工具,其性质与特性一直是学习与研究的核心内容之一。当我们深入探索函数的奥秘时,“函数的拐点”这一概念便显得尤为重要,它不仅是函数图像形态转变的关键点,也是理解函数变化趋势、极值分布乃至实际应用中优化问题的基础。本文将从多个维度解析“函数的拐点是什么”,带领读者走进这一既抽象又具体的数学概念世界。
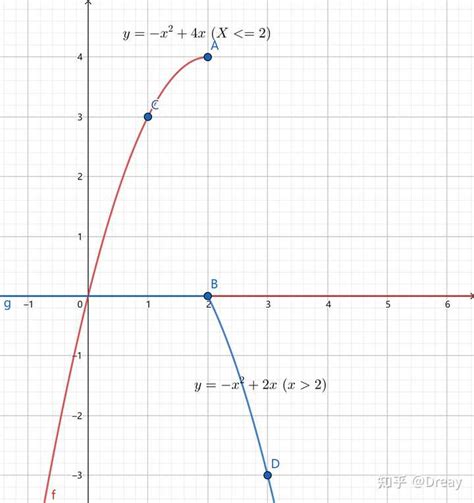
一、拐点的直观认识
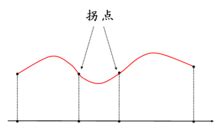
首先,我们尝试通过直观的图像来理解拐点。想象一条平滑的曲线,在大多数情况下,曲线要么持续上升(斜率为正),要么持续下降(斜率为负),或者在某一点处达到极值后改变其升降方向。而拐点,正是这条曲线上那些“转弯”的点,即函数从凹向一侧转变为凸向另一侧,或从凸向一侧转变为凹向另一侧的地方。在图像上,这表现为曲线在该点处曲率的变化。
二、拐点的数学定义
数学上,对于可导函数$f(x)$,如果在某点$x_0$的邻域内,当$x$从左侧趋近于$x_0$时,函数的一阶导数$f'(x)$单调递增(或递减),而从右侧趋近于$x_0$时,$f'(x)$单调递减(或递增),则称$x_0$为函数$f(x)$的拐点(或称为拐点横坐标)。更严格地说,若$f''(x)$(即$f'(x)$的导数,也称二阶导数)在$x_0$处存在且变号(由正变负或由负变正),则$x_0$是$f(x)$的拐点。这里,二阶导数$f''(x)$的符号变化反映了曲线凹凸性的变化,是判断拐点存在与否的重要依据。
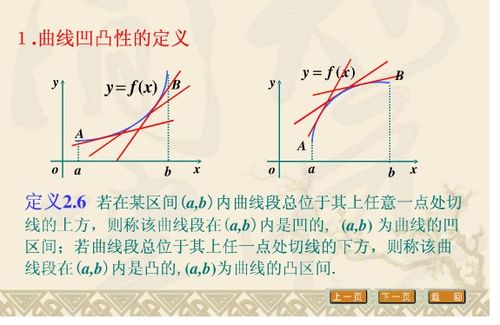
三、拐点的性质与求解
1. 性质:拐点处,函数图像由凹变凸或由凸变凹,对应着二阶导数$f''(x)$的零点且在该点两侧异号。此外,拐点不一定是极值点,但极值点两侧如果存在不同的凹凸性,则该极值点也是拐点。
2. 求解:求解拐点的一般步骤是首先求出函数的二阶导数$f''(x)$,然后令$f''(x)=0$,解出可能的拐点横坐标。接着,需要检验这些点是否真正满足拐点的定义,即检查在这些点两侧$f''(x)$是否异号。有时,还需通过作图或利用函数的其他性质来辅助判断。
四、拐点的实际应用
拐点理论不仅在数学分析中具有重要地位,其在实际应用中也展现出强大的生命力。以下是一些典型的应用场景:
1. 经济学中的供需分析:在供需曲线中,拐点可能代表市场供需平衡点的变化,对于制定价格策略、预测市场趋势具有重要意义。
2. 物理学中的运动分析:在研究物体运动轨迹时,加速度的拐点(即二阶导数零点)对应着物体运动状态的显著变化,如从加速到减速或从减速到加速的转变点。
3. 工程学中的优化设计:在结构力学、材料科学等领域,通过寻找目标函数的拐点,可以实现结构强度的最大化、材料消耗的最小化等优化目标。
4. 生物学中的生长模型:在生物种群增长模型中,拐点可能代表种群增长速率的转折点,对于预测种群数量变化、制定保护策略至关重要。
五、结语
综上所述,函数的拐点作为函数图像形态转变的关键点,其定义、性质及求解方法不仅加深了我们对函数本质的理解,更在多个领域展现了其广泛的应用价值。通过深入学习和掌握拐点的相关知识,我们不仅能更好地解决数学问题,还能在实际应用中灵活运用,为科学研究和生产生活提供有力支持。在未来的学习和探索中,让我们继续保持好奇心,勇攀数学高峰,发现更多未知的奥秘。
-
 高等数学入门:曲线拐点的定义与求解方法资讯攻略11-08
高等数学入门:曲线拐点的定义与求解方法资讯攻略11-08 -
 揭秘:轻松求解曲线拐点的绝妙方法资讯攻略11-15
揭秘:轻松求解曲线拐点的绝妙方法资讯攻略11-15 -
 拐点:是点还是坐标的辨析资讯攻略12-07
拐点:是点还是坐标的辨析资讯攻略12-07 -
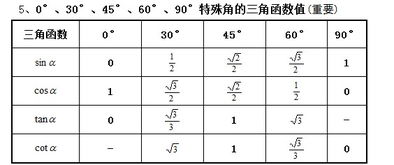 揭秘:三角函数值到底代表着什么?资讯攻略12-03
揭秘:三角函数值到底代表着什么?资讯攻略12-03 -
 掌握Excel电子表格:揭秘高效办公的八大必备函数资讯攻略11-20
掌握Excel电子表格:揭秘高效办公的八大必备函数资讯攻略11-20 -
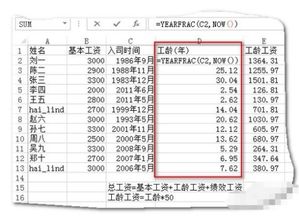 Excel技巧:轻松计算工龄或年龄,揭秘YEARFRAC函数的妙用资讯攻略11-04
Excel技巧:轻松计算工龄或年龄,揭秘YEARFRAC函数的妙用资讯攻略11-04












