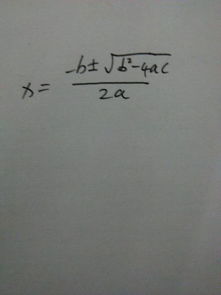探究:“x - 15 4x”能否构成一个数学方程?
在数学的世界里,我们经常会遇到各种各样的表达式和等式,它们构成了数学语言的基础。其中,“方程”这一概念尤为重要,它是连接未知数与实际问题的桥梁,让我们能够求解出未知数的具体值。今天,我们就来探讨一个具体的数学问题:“x - 15 4x是方程吗?”为了深入理解这个问题,我们需要从方程的定义出发,逐步分析这个表达式的构成和特点。

首先,我们要明确什么是方程。简单来说,方程就是一个包含未知数和已知数的等式。这个等式表示了未知数(通常用字母x、y、z等表示)和已知数(或称为常数)之间的关系。方程的主要特点是等号两边相等,且至少含有一个未知数。根据这个定义,我们可以开始分析“x - 15 4x”这个表达式。
乍一看,“x - 15 4x”似乎有些混乱,因为它没有明确的运算符号来分隔各个部分。但我们可以尝试通过添加适当的运算符号来解读它。如果我们将这个表达式理解为“x - 15 + 4x”(即假设中间缺少了一个加号),那么它就变成了一个含有未知数的数学表达式。接下来,我们需要判断这个表达式是否满足方程的定义。
为了使其成为一个方程,我们需要在这个表达式的基础上添加一个等号,并给出等号右边的值。如果我们假设等号右边的值为0(这是数学中常见的假设,因为当方程等于0时,我们可以更容易地找到未知数的解),那么这个表达式就变成了“x - 15 + 4x = 0”。现在,我们可以清晰地看到,这是一个包含未知数x的等式,因此它满足方程的定义。
然而,如果我们不添加等号或等号右边的值,那么“x - 15 4x”(即使我们假设中间是加号)就只是一个数学表达式,而不是一个方程。在数学中,表达式和方程是两个不同的概念。表达式通常用于表示某个量或关系,而方程则用于求解未知数。
现在,让我们进一步分析这个特定的表达式“x - 15 + 4x”。如果我们将其整理为一个更简洁的形式,就可以得到“5x - 15”。虽然这个表达式仍然不是一个方程(因为它没有等号),但它已经是一个更易于理解和操作的数学形式。如果我们想要将其转换为一个方程,我们只需要添加一个等号和一个等号右边的值即可。例如,“5x - 15 = 0”或“5x - 15 = 10”都是有效的方程。
接下来,我们探讨一下这个表达式(或方程)可能的应用场景。在数学学习中,方程通常用于解决实际问题。例如,在物理学中,我们可能会用方程来描述物体的运动状态;在经济学中,我们可能会用方程来预测市场的变化;在日常生活中,我们也可能会用方程来计算购物时的折扣或分期付款的金额等。虽然“x - 15 + 4x”这个具体的表达式看起来很简单,但它也可以被应用于各种实际问题中。
例如,假设我们有一个数学问题:一个数的5倍减去15等于某个给定的值(比如0或10)。为了求解这个问题,我们可以将这个数学关系表示为一个方程,即“5x - 15 = 给定值”。然后,我们可以通过代数运算来求解未知数x的值。这个过程不仅能够帮助我们找到问题的答案,还能够培养我们的逻辑思维和解决问题的能力。
此外,我们还可以从这个表达式中汲取一些数学上的启示。首先,它提醒我们注意数学表达式的准确性和清晰性。在数学中,一个小小的符号错误或遗漏都可能导致整个表达式的意义发生巨大的变化。因此,我们在书写和解读数学表达式时需要格外小心。其次,它展示了数学表达式的灵活性和可变性。通过添加或删除一些元素(如等号、等号右边的值等),我们可以将一个表达式转换为一个方程,或者将一个方程转换为一个更复杂的表达式。这种灵活性使得数学成为了一个充满无限可能性的领域。
最后,我们来总结一下关于“x - 15 4x是方程吗?”这个问题的答案。从严格意义上来说,“x - 15 4x”本身并不是一个方程,因为它没有等号来连接两个相等的数学量。但是,如果我们通过添加适当的运算符号和等号来完善这个表达式,那么它就可以变成一个有效的方程。因此,在判断一个表达式是否是方程时,我们需要仔细审视其结构和组成要素,以确保它满足方程的定义。
综上所述,“x - 15 4x”这个表达式虽然看起来简单,但它却蕴含了丰富的数学知识和应用价值。通过对其进行深入的分析和探讨,我们不仅可以更好地理解方程的概念和定义,还可以发现数学中的奥秘和乐趣。希望这篇文章能够帮助那些对“x - 15 4x是方程吗?”这个问题感兴趣的读者更好地理解这个问题,并激发他们对数学学习的热情和兴趣。
- 上一篇: 2024龙年贺词押韵怎么写?
- 下一篇: 揭秘!TF口红究竟是什么高端品牌?
-
 整式方程的定义与解析资讯攻略02-18
整式方程的定义与解析资讯攻略02-18 -
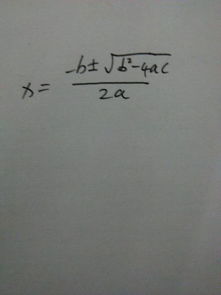 揭秘:掌握解方程的六大关键公式!资讯攻略11-09
揭秘:掌握解方程的六大关键公式!资讯攻略11-09 -
 揭秘一元二次方程的多样化形态资讯攻略11-17
揭秘一元二次方程的多样化形态资讯攻略11-17 -
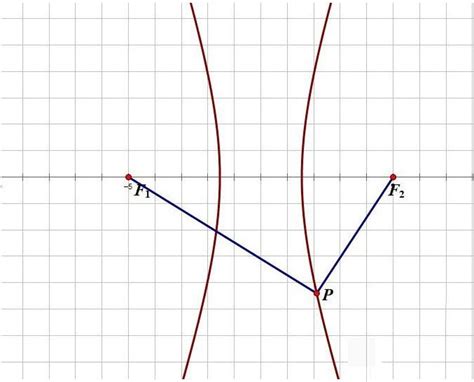 探索VB编程:绘制迷人的双曲螺线艺术资讯攻略10-29
探索VB编程:绘制迷人的双曲螺线艺术资讯攻略10-29 -
 氧化铜与稀盐酸的化学反应方程式资讯攻略02-24
氧化铜与稀盐酸的化学反应方程式资讯攻略02-24 -
 如何解决一元三次方程?资讯攻略11-09
如何解决一元三次方程?资讯攻略11-09