余弦定理如何证明？

揭秘几何学的瑰宝：余弦定理的详尽证明与魅力探索

在浩瀚的数学海洋中，余弦定理犹如一颗璀璨的明珠，以其独特的魅力和广泛的应用，吸引了无数数学爱好者的目光。这个定理不仅连接了三角形的边长与角度，更是几何学、三角学和代数之间的桥梁。今天，就让我们一同深入探索余弦定理的证明过程，揭开它神秘的面纱，领略其背后的数学之美。

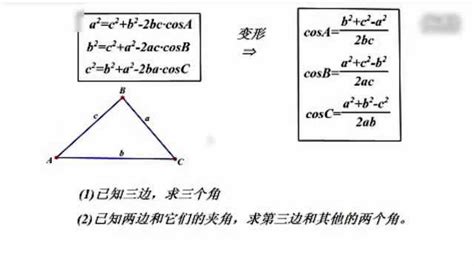
余弦定理，这个在数学课本上频繁出现的公式，其表述简洁明了：在任意三角形ABC中，边a、b、c分别对应角A、B、C，则有a²=b²+c²-2bc*cosA，同理可得b²=a²+c²-2ac*cosB和c²=a²+b²-2ab*cosC。这三个等式共同构成了余弦定理的核心内容，它们揭示了三角形边长与角度之间的内在联系。

那么，这个定理是如何得出的呢？我们首先要明确的是，余弦定理的证明方法有多种，其中最为常见和直观的是几何法和向量法。接下来，我们将分别介绍这两种证明方法，带你领略余弦定理的证明之美。

几何法证明余弦定理

几何法证明余弦定理，主要是通过构造辅助图形，利用三角形的全等、相似等性质进行推导。以下是一个典型的几何法证明过程：

1. 构造辅助线：在三角形ABC中，过点C作CD垂直于AB于点D，得到直角三角形ADC和直角三角形BDC。

2. 应用勾股定理：在直角三角形ADC中，有AD²+CD²=AC²；在直角三角形BDC中，有BD²+CD²=BC²。

3. 将两式相加：将上述两个等式相加，得到AD²+BD²+2CD²=AC²+BC²。由于AD+BD=AB，所以我们可以将上式改写为AB²+2CD²=AC²+BC²。

4. 利用余弦函数：注意到在三角形ABC中，cosA=CD/AC，所以CD=AC*cosA。将这个结果代入上式，得到AB²=AC²+BC²-2AC*BC*cosA，即a²=b²+c²-2bc*cosA。

通过上述步骤，我们成功地利用几何法和勾股定理证明了余弦定理的一个等式。同理，我们可以构造类似的辅助图形，证明其余两个等式。

向量法证明余弦定理

向量法证明余弦定理，则是利用了向量的数量积性质。向量法不仅简洁明了，而且具有更广泛的适用性。以下是一个向量法证明余弦定理的过程：

1. 设定向量：在三角形ABC中，设向量AB=c，向量AC=b，向量BC=a（注意这里的向量表示与边长表示的区别）。

2. 利用数量积性质：根据向量的数量积性质，有b·c=|b|*|c|*cosA。同时，我们知道b-c=a，即向量AC减去向量AB等于向量BC。

3. 对等式两边平方：对等式b-c=a两边平方，得到(b-c)²=a²。展开后得到b²+c²-2b·c=a²。

4. 代入数量积结果：将b·c=|b|*|c|*cosA代入上式，得到b²+c²-2|b|*|c|*cosA=a²。由于|b|、|c|分别等于边长b、c，所以我们可以将上式改写为b²+c²-2bc*cosA=a²，即余弦定理的一个等式。

向量法的证明过程简洁明了，直接利用了向量的数量积性质和等式变换，避免了复杂的几何构造和推导。这也是向量法在数学证明中备受推崇的原因之一。

余弦定理的应用与魅力

余弦定理不仅在理论上具有重要意义，而且在实际应用中发挥着巨大作用。以下是一些余弦定理的应用场景：

1. 天文学：在天文学中，余弦定理被用于计算天体之间的距离和角度。例如，通过观测两个天体之间的夹角和它们到地球的距离，可以利用余弦定理求出它们之间的实际距离。

2. 工程学：在工程学中，余弦定理被广泛应用于结构设计、材料力学等领域。例如，在桥梁、塔吊等结构的设计中，需要利用余弦定理计算结构的稳定性和承载力。

3. 物理学：在物理学中，余弦定理被用于解决力学、电磁学等问题。例如，在弹性力学中，可以利用余弦定理计算物体的应力和应变；在电磁学中，可以利用余弦定理计算电场和磁场的分布。

4. 日常生活