余弦定理有哪些证明方法？

在数学领域，余弦定理占据着举足轻重的地位，它是解决三角形问题的重要工具之一。在探讨余弦定理的证明方法时，我们不仅能深入理解这一几何定理的本质，还能借此机会领略到数学的严密逻辑和美妙证明。本文将围绕“余弦定理的证明方法”展开，通过向量法、几何法以及复数法等多种途径，揭示余弦定理的深刻内涵。

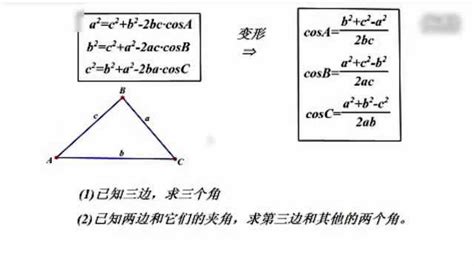
首先，我们简要回顾一下余弦定理的基本内容。对于任意三角形ABC，其中a、b、c分别为三角形的三边，A、B、C分别为三角形的三个角，且角A与边a相对，角B与边b相对，角C与边c相对。余弦定理表述为：a²=b²+c²-2bc cos A，b²=a²+c²-2ac cos B，c²=a²+b²-2ab cos C。这一公式揭示了三角形任意一边的平方等于其他两边的平方和减去这两边与其夹角的余弦的积的两倍。

一、向量法证明余弦定理

向量法是证明余弦定理的一种现代而简洁的方法。在平面直角坐标系中，我们可以将三角形的顶点视为向量，并利用向量的数量积性质进行推导。

设三角形ABC的三个顶点A、B、C对应的向量分别为a、b、c（此处向量a、b、c与三角形的边a、b、c同名，但意义不同，需注意区分）。根据向量的数量积公式，有a·b=|a|×|b|×cos A，其中“·”表示数量积，“|a|”表示向量a的模（即长度）。

首先，我们考虑向量AB（即向量b-向量a）与向量AC（即向量c-向量a）的数量积。根据数量积的定义和性质，有：

(b-a)·(c-a)=|b-a|×|c-a|×cos A

展开后得到：

b·c-a·b-a·c+a²=|b-a|×|c-a|×cos A

由于|b-a|即为BC的长度（即a的对应边），|c-a|即为AB的长度（即c的对应边，但方向相反，不影响长度），所以上式可以进一步写为：

b·c-a·b-a·c+a²=bc cos A

又因为a·b=|a|×|b|×cos B，a·c=|a|×|c|×cos C，代入上式得：

|b|×|c|×cos(180°-B)-|a|×|b|×cos B-|a|×|c|×cos C+|a|²=bc cos A

化简后得到：

|b|×|c|×cos B-|a|×|c|×cos C+|a|²+|b|×|c|×cos(180°-A)=bc cos A

由于cos(180°-θ)=-cos θ，上式可进一步化简为：

|b|×|c|×cos A-|a|×|c|×cos C+|a|²-|b|×|c|×cos A=bc cos A

化简后得到：

|a|²=|b|²+|c|²-2|b|×|c|×cos A

即a²=b²+c²-2bc cos A，这就证明了余弦定理。

二、几何法证明余弦定理

几何法是传统的证明方法，通过构造辅助线并利用三角形的性质和相似关系进行推导。

在三角形ABC中，过点C作AB的垂线，交AB于点D。则根据勾股定理，有AC²=AD²+CD²，BC²=BD²+CD²。

设AD=x，BD=y，CD=h，则有：

AC²=x²+h²，BC²=y²+h²

又因为x+y=AB=c，所以y=c-x。

在三角形ADC中，根据余弦的定义，有cos A=AD/AC=x/AC。所以AC=x/cos A。

将AC代入AC²=x²+h²中，得到：

(x/cos A)²=x²+h²

化简后得到：

h²=x²/cos² A-x²=(1-cos² A)/cos² A×x²=sin² A/cos² A×x²=tan² A×x²

即h=tan A×x。

将h代入BC