如何精确计算年利率
在探讨年利率的计算方式时,我们首先需要明确几个核心概念:年利率、本金、利息以及贷款或存款的期限。年利率,简而言之,就是资金在一年内所获得的利息率,是衡量资金时间价值的重要指标之一。无论是对于储户来说,希望通过存款获得收益,还是对于借款人而言,在规划贷款偿还时,准确计算年利率都显得尤为重要。
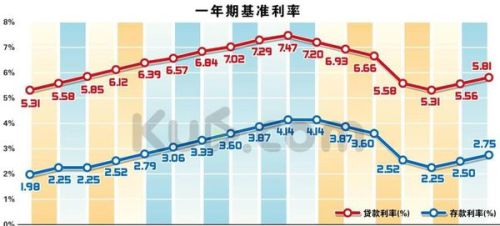
年利率的基础定义
年利率,通常表示为百分数形式,如5%或0.05(小数形式),它反映了资金在一年内相对于本金增值或负担的比例。这一比率可能因银行、金融机构、市场条件以及产品类型(如定期存款、房屋贷款、个人消费贷款等)而异。

利息的基本计算原理
要计算年利率下的利息,我们首先需要知道三个基本要素:本金(P),年利率(r,通常转换为小数形式),以及时间(t,单位为年)。利息(I)的计算公式为:

\[ I = P \times r \times t \]
本金(P):初始投资或贷款金额。
年利率(r):资金每年增值或负担的比例,需转换为小数形式进行计算,例如5%应写为0.05。
时间(t):资金被持有或借用的年数。
不同类型的年利率计算
1. 简单年利率
在简单利息的计算中,利息仅基于原始本金计算,不考虑利息本身再产生利息(即复利效应)。计算公式直接采用上述的 \(I = P \times r \times t\)。这种计算方式相对简单直接,常见于某些短期贷款或特定类型的储蓄产品中。
2. 复利年利率
复利则是一种更为复杂的计算方式,它允许利息在每个计息周期(如每年、每季、每月等)结束时加入本金,从而在下一个计息周期中继续产生利息。对于年复利而言,若年利率为r,本金为P,n年后的总金额(A)包括本金与累积利息,可以通过以下公式计算:
\[ A = P \times (1 + r)^n \]
其中,\(A - P\) 即为n年内的总利息。复利效应使得资金在长期内能够显著增值,是投资与理财中不可忽视的力量。
实际应用举例
假设某人将10,000元存入银行,年利率为3%(即0.03),存款期限为3年。
简单利息计算:
利息 = \(10,000 \times 0.03 \times 3 = 900\)元
3年后总金额 = 本金 + 利息 = \(10,000 + 900 = 10,900\)元
复利利息计算(以年为单位复利):
3年后总金额 = \(10,000 \times (1 + 0.03)^3 = 10,927.27\)元
利息 = 总金额 - 本金 = \(10,927.27 - 10,000 = 927.27\)元
通过对比可以看出,尽管两种方法的本金和年利率相同,但由于复利效应,使用复利计算时最终获得的利息和总金额会更高。
注意事项
利率变动:实际情况下,年利率可能因市场波动、政策调整或合同条款而变动,因此在进行长期规划时需考虑这一因素。
费用与税收:部分金融产品在计算最终收益时还需考虑管理费、手续费及可能的税收影响。
利率转换:在比较不同金融机构或产品时,注意将年利率转换为相同的时间单位(如日利率、月利率转换为年利率)进行比较,以获取准确信息。
综上所述,年利率的计算是金融基础知识的重要组成部分,它不仅关系到个人与企业的财务规划,也是评估投资与借贷成本效益的关键指标。通过掌握年利率的计算方法及其应用场景,我们能更好地做出经济决策,优化资金配置,实现财富的稳健增长。
-
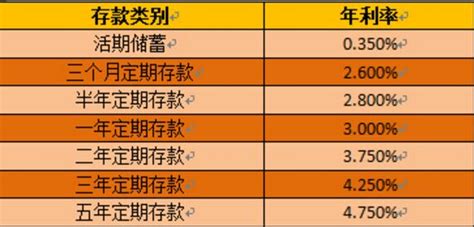 轻松学会:如何计算年利率,让你的理财更明智!资讯攻略10-24
轻松学会:如何计算年利率,让你的理财更明智!资讯攻略10-24 -
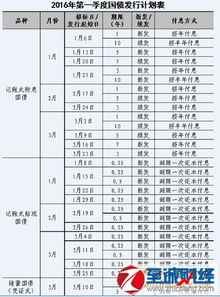 详解月利率与年利率的差异资讯攻略10-31
详解月利率与年利率的差异资讯攻略10-31 -
 揭秘贷款计算的奥秘:轻松掌握贷款算法资讯攻略11-18
揭秘贷款计算的奥秘:轻松掌握贷款算法资讯攻略11-18 -
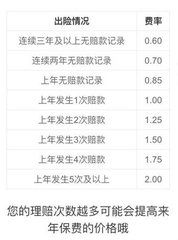 如何精确计算汽车保险费用资讯攻略10-29
如何精确计算汽车保险费用资讯攻略10-29 -
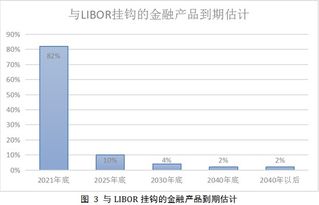 揭秘:SHIBOR与LIBOR究竟是什么?资讯攻略02-13
揭秘:SHIBOR与LIBOR究竟是什么?资讯攻略02-13 -
 揭秘:结息交易到底是什么?资讯攻略12-06
揭秘:结息交易到底是什么?资讯攻略12-06












