1弧度对应的角度是多少，怎么计算？

在数学的广阔领域中，角度与弧度是描述平面角大小的两种基本单位，它们各自拥有独特的定义和应用场景，却又在特定的条件下相互转换，展现出数学中和谐统一的美。本文将从历史背景、定义解析、几何意义、实际应用以及转换公式的推导等多个维度，深入探讨“1弧度等于多少角度”这一问题，旨在帮助读者全面理解弧度与角度之间的关系。

历史背景：从直观到抽象

角度的概念源远流长，早在古代文明中，人们就通过观察太阳的位置、星辰的运行来划分天空，形成了最初的角度观念。古埃及人利用角度测量土地，巴比伦人则发明了六十进制来细分圆周，这些都为后来的角度体系奠定了基础。而弧度的概念则相对较晚出现，它起源于17世纪的欧洲，随着微积分学的发展，数学家们开始寻求一种更为自然、便于计算的角度度量方式，弧度制应运而生。欧拉、莱布尼茨等数学大师的工作，极大地推动了弧度制的普及和应用，使其成为现代数学和物理学中不可或缺的工具。

定义解析：角度与弧度的本质

角度的定义：角度是最直观、最常用的角度量单位，它基于圆周的1/360作为一度，记作°。角度制易于理解和使用，尤其适合日常生活中的测量和计算，如时钟的指针位置、地理坐标等。

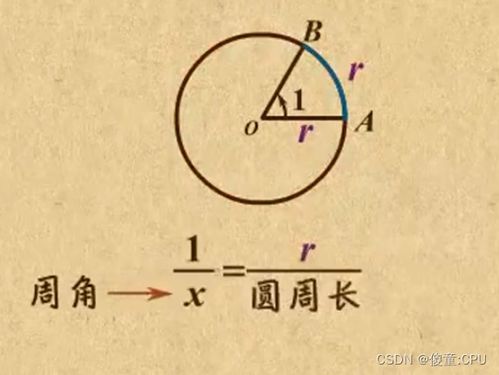
弧度的定义：弧度制则是一种基于圆的自然属性定义的度量方式。一个完整的圆周对应的弧度数为2π（π约等于3.14159...），即半径为r的圆上，弧长等于r的弧所对应的圆心角为1弧度。这一定义不仅简洁，而且与圆的几何性质紧密相连，为微积分中的极限、导数、积分等概念提供了自然的数学语言。

几何意义：直观理解弧度与角度

在几何学中，角度和弧度都是描述两条射线与其共同的端点（即顶点）之间夹角大小的量度。角度制通过将一个圆周等分为360份，每份定义为1度，直观易懂；而弧度制则是基于圆的弧长与半径的比例关系，将圆周角定义为2π弧度，这种定义方式使得弧长、半径与圆心角之间建立了直接的数学联系。

例如，考虑一个半径为r的圆，若某段弧的长度恰好等于r，则这段弧所对应的圆心角即为1弧度。通过这一几何直观，我们可以发现，当半径r增大时，虽然弧的实际长度增加了，但对应的圆心角（以弧度计）保持不变，这体现了弧度制在描述不同尺度圆上角的大小时具有的一致性。

实际应用：弧度制的优势

在实际应用中，弧度制因其与圆的自然属性相契合，展现出诸多优势。在物理学中，特别是涉及周期性运动（如简谐振动、圆周运动）的问题时，使用弧度制可以大大简化方程，使得求解过程更加直观和高效。在工程学领域，如机械设计、电子信号处理等，弧度制也是不可或缺的数学工具，它使得旋转运动的分析和计算更加精确和便捷。

此外，在计算机科学中，弧度制也是图形处理、计算机动画等领域的基础。由于计算机内部通常采用浮点数表示数值，而弧度制在数值计算中的稳定性和精度优于角度制，因此成为这些领域中的首选。

转换公式的推导：1弧度等于多少角度

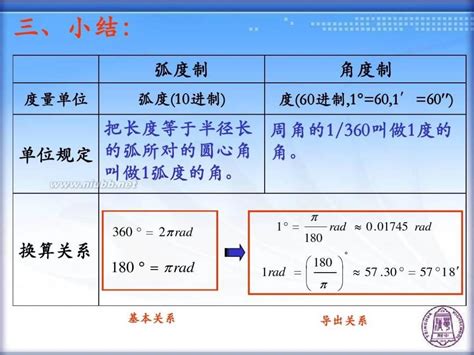
要解答“1弧度等于多少角度”这一问题，我们需要找到弧度与角度之间的转换公式。根据弧度制的定义，一个完整的圆周对应的弧度数为2π，而在角度制中，这个圆周被划分为360度。因此，弧度与角度之间的转换关系可以表示为：

\[ \text{弧度} = \left( \frac{\pi}{180} \right) \times \text{角度} \]

\[ \text{角度} = \left( \frac{180}{\pi} \right) \times \text{弧度} \]

将1弧度代入上述公式中，即可求得对应的角度值：

\[ 1 \text{弧度} = \left( \frac{180}{\pi} \right) \times 1 \approx 57.2957795131^\circ \]

这一结果揭示了弧度与角度之间的具体数量关系，也说明了为什么在数学和物理学的许多分支中，弧度制能够提供更简洁、更自然的数学表达。

深入理解：弧度制的深层意义

弧度制不仅仅是一种数学上的度量单位，它更深层次地反映了数学与物理世界的内在联系。在微积分中，弧度制使得函数的导数、积分等运算更加直观和易于理解。例如，在求圆的切线斜率（即导数）时，若采用弧度制，则可直接利用三角函数的导数公式，而无需额外的转换步骤。此外，在复分析、傅里叶变换等高级数学理论中，弧度制也是不可或缺的基础。

从哲学层面看，弧度制体现了数学追求简洁、和谐的美学理念。它通过对圆的自然属性的抽象和提炼，构建了一个既符合逻辑又便于计算的数学体系，展现了人类智慧在探索自然规律过程中的创造力和洞察力。

结语

综上所述，1弧度等于约57.2957795131度，这一转换关系不仅是一个简单的数学事实，更是连接角度制与弧度制两大度量体系的桥梁。通过对角度与弧度的定义、几何意义、实际应用以及转换公式的深入探讨，我们不难发现，两者各有千秋，共同构成了数学中描述角大小的两把“尺子”。在不同的应用场景下，选择最合适的度量单位，不仅能够简化计算，还能更深刻地揭示问题的本质。因此，在学习和实践中，我们应当灵活掌握这两种度量方式，以数学的眼光洞察世界，以数学的思维解决问题。