探索弧度的奥秘：轻松学会计算方法

弧度是数学中一个非常重要的概念，尤其是在三角学和微积分等领域中，其应用十分广泛。对于初学者来说，理解并计算弧度可能会有些困难，但只要我们掌握了相关的基础知识和计算方法，就能够轻松应对。下面，我们就来详细探讨一下弧度的计算方法及其相关知识。

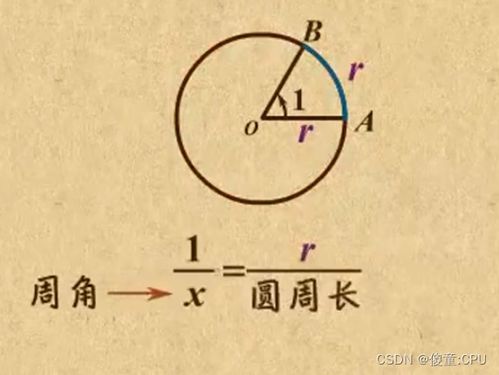
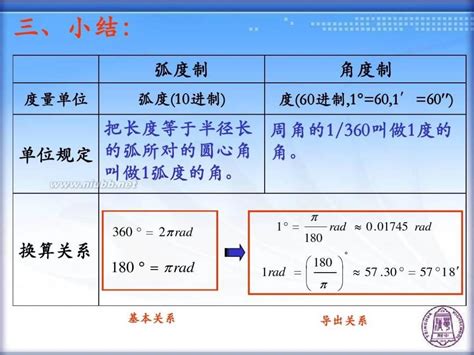
首先，我们需要明确什么是弧度。弧度是一种度量角大小的方式，它与角度制不同，但两者之间可以相互转换。弧度的定义是基于圆的，一个完整的圆周对应的弧度值是2π（π是一个无理数，约等于3.14159）。因此，我们可以说，一个圆的弧度制表示就是2π弧度，或者说是360度等于2π弧度。

那么，我们如何计算一个给定角度的弧度值呢？这里有一个简单的公式可以帮助我们进行转换：弧度 = 角度 × π/180。这个公式的来源是基于弧度制和角度制之间的比例关系。例如，如果我们想知道90度对应的弧度是多少，就可以使用这个公式进行计算：90 × π/180 = π/2 弧度。同样地，我们也可以用这个公式将弧度转换回角度，只需要将公式中的角度和弧度互换位置，并相应地调整比例系数即可：角度 = 弧度 × 180/π。

除了这种基于比例的转换方法外，我们还可以通过观察单位圆上的弧长来直观理解弧度的概念。单位圆是一个半径为1的圆，它可以帮助我们更直观地理解角度和弧度之间的关系。在单位圆上，一个角度对应的弧长就是该角度的弧度值。例如，当我们说一个角度是π/2弧度时，我们实际上是指在单位圆上，从正x轴开始，逆时针旋转到正y轴所经过的弧长是π/2。

在理解了弧度的基本概念和计算方法后，我们就可以开始解决一些具体的数学问题了。例如，计算三角函数在给定弧度下的值。三角函数是数学中一类重要的函数，包括正弦函数、余弦函数、正切函数等。这些函数在弧度制下的定义和性质与在角度制下有所不同，但它们的计算方法却更加简洁和直观。例如，正弦函数sin(x)在弧度制下的定义是：对于单位圆上任意一点P(x,y)，其纵坐标y就是sin(x)的值。同样地，余弦函数cos(x)的定义是点P的横坐标x的值。这些定义使得我们在计算三角函数值时，可以直接利用单位圆上的几何关系，而无需进行繁琐的角度制转换。

此外，弧度在计算圆的弧长、扇形的面积等方面也有重要应用。例如，如果我们知道一个圆的半径r和一个角度θ（以弧度为单位），我们就可以使用这个公式来计算对应的弧长：弧长 = r × θ。同样地，如果我们想计算一个扇形的面积，也可以利用弧度和半径来计算：扇形面积 = (1/2) × r^2 × θ。这些公式在解决实际问题时非常有用，可以帮助我们更快速地得到结果。

除了上述基本应用外，弧度还在微积分等高级数学领域中发挥着重要作用。在微积分中，我们经常需要处理与导数、积分等相关的数学问题。而弧度制在这些问题的求解过程中往往更加方便和直观。例如，在计算三角函数的导数时，我们会发现使用弧度制可以使得公式更加简洁和易于记忆。同样地，在计算某些类型的积分时，弧度制也能够让我们更快地找到解决方法。

此外，弧度在计算物理学中的一些问题时也非常有用。例如，在力学中，我们经常需要处理与旋转和振动相关的问题。而这些问题往往涉及到角度和弧度的计算。通过掌握弧度的计算方法，我们可以更加准确地描述和分析这些问题，并找到相应的解决方案。

当然，对于初学者来说，掌握弧度的计算方法并不是一件容易的事情。但只要我们不断地练习和实践，就能够逐渐熟悉并掌握这一技能。同时，我们还需要注意一些常见的错误和陷阱。例如，在计算弧度时，我们一定要注意角度的单位是否正确；在转换弧度制时，我们也需要注意比例系数的正确性；在使用三角函数表或计算器进行计算时，我们还需要注意输入的角度或弧度单位是否与表或计算器要求的单位一致等。

总的来说，弧度是一个非常重要的数学概念，它在数学、物理学和其他领域中都有广泛的应用。通过掌握弧度的计算方法，我们可以更好地理解和解决与角度和旋转相关的问题，并为进一步学习更高级的数学知识和物理概念打下坚实的基础。因此，我们应该认真学习并熟练掌握弧度的计算方法，以便在未来的学习和工作中能够更好地应用这一技能。