角度制和弧度制之间如何转换？

在数学的世界中，角度与弧度是衡量角大小的两种基本单位，它们如同度量衡中的米与英尺，虽形式不同，却能在特定的转换规则下相互对应，共同构建起几何学的宏伟殿堂。角度制，这一源自古代文明直观感知的度量方式，以度（°）为基本单位，将一个完整的圆周划分为360度；而弧度制，则是微积分时代诞生的产物，以弧长与半径的比值定义角的大小，更加符合数学运算的内在逻辑。本文将从历史渊源、数学原理、应用实践及思维启迪四个维度，探讨角度制和弧度制之间的转化公式及其深远意义。

历史渊源：从直观到抽象的跨越

角度制的起源可追溯至古埃及、巴比伦等古代文明，人们通过观察太阳的位置变化、季节更替等自然现象，逐渐形成了对圆周分割的直观认识。360度这一数字的选择，或许源于一年中大约360天的近似，或是古代人们对手指关节数的计数习惯，其本质是对自然界周期性现象的一种简化抽象。相比之下，弧度制的概念则要晚得多，它的出现与微积分学的兴起密切相关。17世纪的数学家如莱布尼茨、欧拉等人，在探索曲线的性质、求解微分方程的过程中，发现弧度制能更简洁地表达三角函数的关系，从而推动了弧度制的广泛应用。

数学原理：转换公式的推导与理解

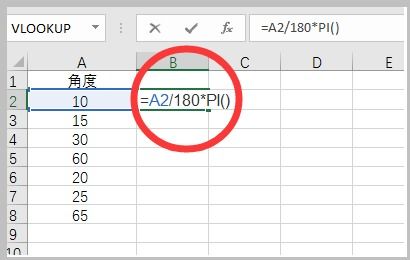
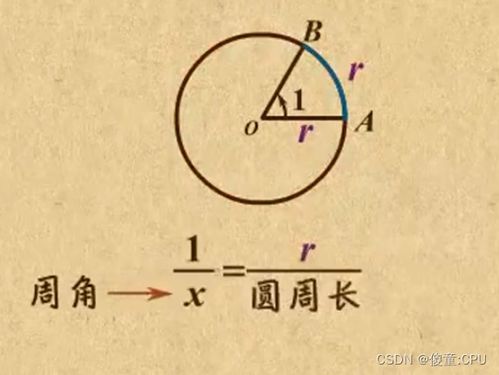
角度制与弧度制之间的转换，其核心在于两者定义的本质差异。角度制以“度”为单位，将圆周等分为360份；而弧度制则以弧长与半径的比值定义角的大小，一个完整的圆周对应弧度为2π。因此，两者之间的转换公式为：

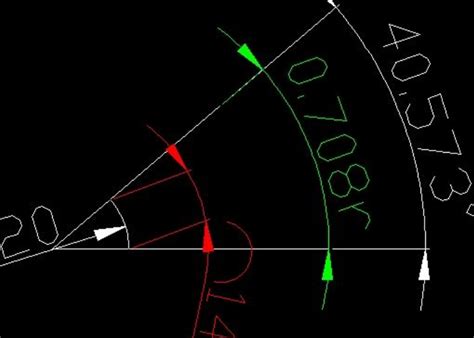
\[ \text{弧度} = \text{角度} \times \frac{\pi}{180} \]

\[ \text{角度} = \text{弧度} \times \frac{180}{\pi} \]

这两个公式看似简单，却蕴含着深刻的数学原理。它们不仅实现了两种度量单位之间的数值转换，更重要的是，它们揭示了不同度量体系下角的本质——无论是基于直观分割的角度制，还是基于几何性质的弧度制，都是对角这一抽象概念的量化表达。通过转换公式，我们能够跨越这两种体系，自由地在不同的数学语境中穿梭，解决各种实际问题。

应用实践：从三角函数到物理学的桥梁

在三角函数领域，弧度制的优势尤为明显。正弦、余弦、正切等三角函数在弧度制下表现出更加简洁的周期性、对称性和微分性质，这些特性对于解决微积分问题、物理波动方程、信号处理等领域的问题至关重要。例如，在物理学中，简谐振动的周期公式T = 2π/ω（ω为角频率），只有在弧度制下才成立，若采用角度制，则需额外引入一个转换因子。此外，在计算机图形学、机器人路径规划等领域，弧度制的连续性和平滑性使得角度的计算更加精确高效，避免了角度制下周期性跳跃带来的不便。

思维启迪：度量背后的哲学思考

角度制与弧度制的转换，不仅是数学技巧的体现，更是对人类认知方式的一次深刻反思。角度制反映了人类对自然界的直观感知和分类思维，它强调整体与部分的关系，体现了人类早期对宇宙秩序的探索和把握。而弧度制则代表了数学抽象和逻辑推理的力量，它揭示了隐藏在直观现象背后的数学规律，推动了科学研究的深入发展。这两种度量方式的并存与转换，启示我们：在认识世界的过程中，既要尊重直观的感知，也要勇于突破传统框架，通过数学的语言去揭示自然的奥秘。

进一步而言，角度制与弧度制的转换公式，还蕴含着一种“桥梁思维”。它教会我们在面对不同体系、不同文化、不同观念时，应学会寻找共通之处，建立沟通的桥梁，实现相互理解和融合。这种思维方式在当今全球化的背景下尤为重要，它鼓励我们以开放的心态，跨越语言和文化的障碍，共同推动人类文明的进步。

结语

综上所述，角度制与弧度制之间的转化公式，不仅是数学中的一个基础概念，更是连接直观与抽象、过去与未来、人类与自然之间的一座桥梁。它让我们在数学的严谨与自然的直观之间找到了平衡点，促进了科学的进步和人类文明的发展。在学习和实践中，深入理解这一转换公式，不仅能够提升我们的数学素养，更能够激发我们对数学、对自然、对人类社会的深刻思考，引领我们走向更加广阔的智慧之旅。