轻松掌握:弧度与角度的换算方法
在数学和物理学中,角度和弧度是两种用来描述旋转量的度量单位。虽然它们看似不同,但在实际应用中可以相互转换。本文旨在简明扼要地介绍如何将弧度换算成角度,帮助读者理解这一重要而基础的概念。
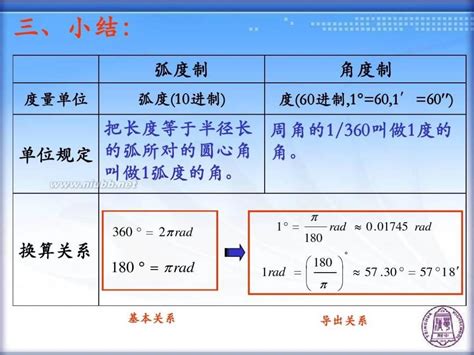
首先,我们要明确弧度与角度的基本概念。角度是一种基于圆周的分割度量方式,通常用一个度(°)符号表示。一个完整的圆周被定义为360度。而弧度,则是一种更为自然的度量方式,它与圆的半径长度紧密相关。弧度以弧长与半径的比值来定义,意味着一个完整的圆周对应的弧度值是2π(约等于6.28)。

理解这两种度量方式的基础之后,我们就可以探讨它们之间的转换公式。弧度转角度的公式非常简洁:角度(°)= 弧度 × (180/π)。这个公式是弧度换算成角度的核心,它表明将弧度值乘以一个常数(180/π)即可得到相应的角度值。

在深入讨论换算过程之前,让我们先通过一个简单的例子来直观感受这个转换。假设我们有一个弧度值为π/2的角,这代表了一个直角(90度)。根据转换公式,π/2 × (180/π) = 90°,正好验证了我们预期的结果。这个例子说明了公式的正确性,并展示了其在实际应用中的便利性。

接下来,为了更全面地掌握换算技巧,我们将通过一个详细的步骤分解,指导读者如何进行换算。
第一步:确定弧度值。这是转换过程的起点,你需要明确待转换的弧度值是多少。
第二步:应用转换公式。将已知的弧度值代入公式,即弧度 × (180/π)。这一步是计算过程的核心,你需要使用计算器来求解(除非你能手动计算π的乘除)。
第三步:得出结果。根据公式计算出的结果即为对应的角度值。注意检查计算结果是否合理,例如,弧度值在0到2π之间(对应0°到360°)时,角度值也应落在这一范围内。
在实际应用中,这个换算过程对于解决涉及圆和角度的问题至关重要。例如,在三角函数的学习中,角度和弧度经常需要相互转换。三角函数,如正弦、余弦和正切,在弧度制下具有更自然的定义和性质。因此,在处理这些问题时,熟练掌握弧度与角度的换算技巧显得尤为重要。
此外,在物理学和工程学领域,弧度制也常被用于描述旋转运动。例如,在机械设计中,电机或涡轮的旋转量通常用弧度来表示。而在这些领域的计算中,有时需要将弧度转换为角度,以便更直观地理解或比较结果。
值得注意的是,虽然角度和弧度在数值上不同,但它们都描述了同一个物理量——旋转量。因此,在进行换算时,我们需要保持对旋转量本质的理解,这有助于我们更准确地运用这些度量单位。
在进一步探讨弧度换算成角度的应用时,我们不得不提到计算器在这一过程中的重要性。现代计算器通常都配备了弧度与角度之间的转换功能,这使得换算过程变得更加快捷和准确。在使用计算器进行换算时,确保已正确设置计算器的角度单位(弧度或角度),以避免计算错误。
除了计算器,一些数学软件和编程语言也提供了弧度与角度之间的转换函数。这些工具和方法为科学家、工程师和数学家们提供了更多的选择和便利,使他们能够更高效地进行数学计算和物理模拟。
此外,对于希望深入了解弧度与角度关系的读者来说,学习一些基础的几何学和三角学知识是非常有益的。这些知识不仅能够帮助他们更好地理解弧度与角度的概念,还能够提升他们在解决复杂数学问题时的能力。
总的来说,弧度换算成角度是一个简单但重要的数学概念,它在数学、物理学和工程学等多个领域都有广泛的应用。通过掌握这个换算技巧,我们能够更好地理解和处理涉及圆和角度的问题,提高我们的计算能力和解决问题的能力。
最后,值得强调的是,虽然弧度与角度之间的转换看似简单,但在实际应用中,我们仍然需要保持谨慎和准确。因为即使是微小的计算错误,也可能导致结果出现较大的偏差。因此,在进行换算时,我们应该始终确保已知条件的准确性,并仔细核对计算结果。
通过本文的介绍,我们希望能够帮助读者理解弧度与角度之间的换算关系,并掌握相应的换算技巧。无论是在学术研究还是实际应用中,这一知识都将为读者提供有力的支持和帮助。希望读者能够珍视这一基础概念,并在未来的学习和工作中不断加以运用和提升。
- 上一篇: 百度极速版怎样进行每日签到?
- 下一篇: 掌握《神庙逃亡2》游戏攻略,轻松玩转!
-
 揭秘:1度与弧度之间的神秘换算关系资讯攻略01-09
揭秘:1度与弧度之间的神秘换算关系资讯攻略01-09 -
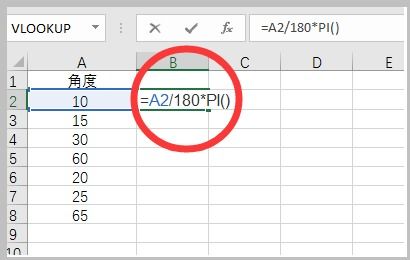 如何将弧度转换为角度?资讯攻略11-09
如何将弧度转换为角度?资讯攻略11-09 -
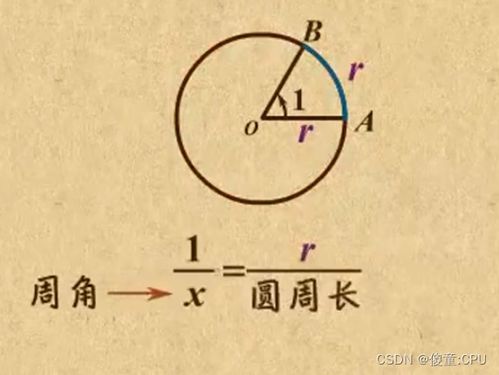 探索弧度的奥秘:轻松学会计算方法资讯攻略11-06
探索弧度的奥秘:轻松学会计算方法资讯攻略11-06 -
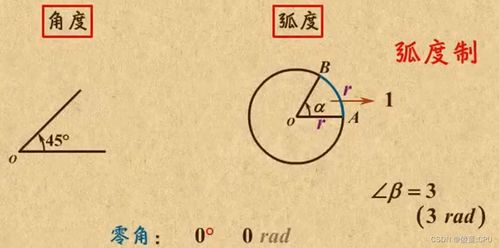 角度与弧度轻松转换秘籍资讯攻略11-25
角度与弧度轻松转换秘籍资讯攻略11-25 -
 Win10计算器中将角度转换为弧度的方法资讯攻略11-09
Win10计算器中将角度转换为弧度的方法资讯攻略11-09 -
 1弧度对应的角度是多少,怎么计算?资讯攻略11-09
1弧度对应的角度是多少,怎么计算?资讯攻略11-09










