揭秘四阶行列式的计算步骤:轻松掌握高阶行列式求解法
四阶行列式是线性代数中的一个重要概念,它在解决许多数学问题和实际问题时都发挥着关键作用。本文将详细介绍四阶行列式的计算方法,并给出具体步骤,以便读者能够清晰理解并掌握这一知识点。
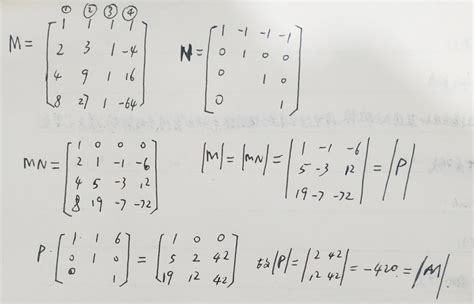
一、基本概念
首先,我们需要明确什么是四阶行列式。四阶行列式是一个4x4的矩阵,由四个行和四个列组成,每个元素都是实数或复数。行列式的值可以通过一系列的计算步骤得出,这个值在数学和物理学中有着广泛的应用。

二、计算步骤
方法一:利用代数余子式
1. 选择元素:

首先,我们选择一个特定的元素,例如a33(第三行第三列的元素),并保留它,同时将第三行的其余元素变为0。

2. 表示行列式:

用代数余子式表示四阶行列式。代数余子式是指去掉某个元素所在的行和列后得到的3x3子矩阵的行列式,余子式前-1的次方为保留的a33的行列数之和。
3. 计算三阶行列式:
接下来,用代数余子式表示三阶行列式,并按照对角法则计算出二阶行列式的结果。对角法则是指,通过计算对角线上的元素乘积减去非对角线上的元素乘积的和,得到二阶行列式的值。
4. 求和:
将上述步骤中得到的所有代数余子式的结果相加,得到四阶行列式的值。
方法二:通过行列变换化简
1. 行列加法:
首先,将第二、三、四列的元素分别加到第一列上,这样可以尝试提取第一列的公因子。
2. 提取公因子:
如果第一列的元素可以提取公因子,则提取出来,将行列式化简。
3. 行变换:
通过行变换,例如第一行乘-1加到第二行,第一行乘-2加到第三行,第一行乘-3加到第四行,使得第一列除了第一个元素外,其余元素均为0。
4. 按列展开:
此时,行列式可以按第一列展开,得到一系列三阶行列式的和。
5. 计算三阶行列式:
对每个三阶行列式进行计算,得到结果后相加,即为四阶行列式的值。
方法三:化为阶梯型行列式
1. 行列变换:
反复使用行列的线性变换,即一行(列)乘以某倍数加到另一行(列)上,直到将行列式化简为阶梯型(上三角、下三角、甚至对角型)的行列式。
2. 计算对角型行列式:
如果行列式化为对角型,则行列式的值等于对角线上元素的乘积。
3. 计算其他类型行列式:
如果行列式化为上三角或下三角型,则行列式的值等于主对角线上元素的乘积(上三角)或副对角线上元素的乘积(下三角)乘以(-1)的(n(n-1))/2次方(n为行列式的阶数)。
三、注意事项
1. 元素位置:
在使用代数余子式时,需要注意元素的位置,以及代数余子式前的符号,这取决于保留的元素所在的行和列。
2. 行列变换的灵活性:
在通过行列变换化简行列式时,需要灵活运用不同的变换方法,以达到化简的目的。
3. 计算的准确性:
在进行具体的计算时,需要仔细核对每一步的计算结果,确保没有计算错误。
4. 行列式的性质:
了解行列式的性质有助于简化计算,例如,行列式中两行(列)互换,结果等于原行列式的相反数;行列式的某一行(列)加上另一行(列)的k倍,结果不变等。
四、实例分析
以线性代数中的一个四阶行列式(1234,2134,3412,4321)为例,展示具体的计算过程。
1. 方法一:
第一行乘(-1)加到第二行,第一行乘(-2)加到第三行,第一行乘(-3)加到第四行,使得第一列只有第一个元素非零。
按第一列展开,得到一系列三阶行列式的和。
分别计算这些三阶行列式的值,并相加,得到最终结果。
2. 方法二:
第二行加到第一行,第三行加到第一行,第四行加到第一行,提取第一行的公因子10。
再将第一行-2倍
- 上一篇: 简单步骤教你如何折叠纸飞镖
- 下一篇: 高效去除蚂蚁的方法
-
 探索线性代数奥秘:方阵行列式的魔力与基本运算性质揭秘资讯攻略10-29
探索线性代数奥秘:方阵行列式的魔力与基本运算性质揭秘资讯攻略10-29 -
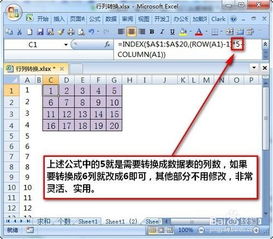 Excel绝技大揭秘:轻松实现行列互换的魔法操作资讯攻略10-25
Excel绝技大揭秘:轻松实现行列互换的魔法操作资讯攻略10-25 -
 加入电动车代理行列,你需满足的金牌条件资讯攻略11-21
加入电动车代理行列,你需满足的金牌条件资讯攻略11-21 -
 揭秘:轻松成为有钱人的秘诀!资讯攻略02-02
揭秘:轻松成为有钱人的秘诀!资讯攻略02-02 -
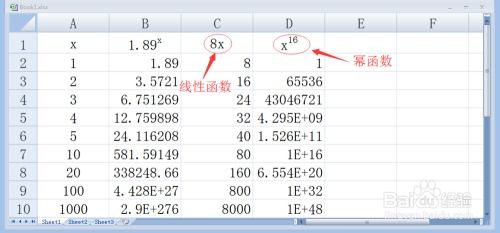 Excel中轻松掌握指数函数求解技巧资讯攻略11-01
Excel中轻松掌握指数函数求解技巧资讯攻略11-01 -
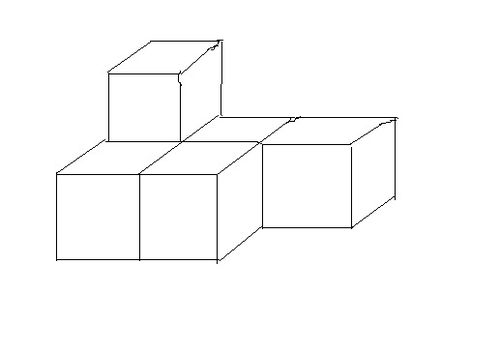 揭秘正方体体积的求解奥秘资讯攻略11-16
揭秘正方体体积的求解奥秘资讯攻略11-16












