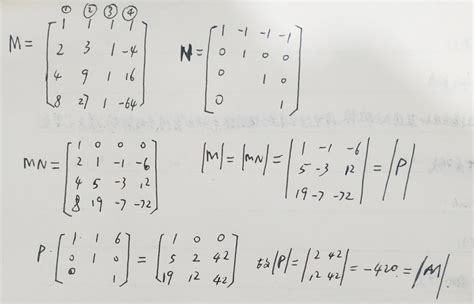探索线性代数奥秘:方阵行列式的魔力与基本运算性质揭秘
线性代数作为数学的一个重要分支,广泛应用于计算机科学、物理学、工程学等多个领域。方阵的行列式及其基本运算性质是线性代数中的核心概念之一,对于理解和解决线性方程组、矩阵的特征值等问题具有重要意义。本文将详细介绍方阵的行列式及其基本运算性质,帮助读者掌握这一重要工具。

首先,我们需要明确什么是方阵。方阵是指行数和列数相等的矩阵,通常用大写字母表示,如A、B等。对于一个n阶方阵A,其行列式记作|A|或det(A),是一个重要的数值量,它不仅反映了矩阵的某种性质,还在矩阵的运算中起着关键作用。

行列式的计算通常使用递归的方法,即通过拉普拉斯定理(也称为按行(列)展开定理)来计算。对于一个n阶方阵A,我们可以选择任意一行或一列,将其元素与对应的代数余子式相乘后求和,即可得到行列式的值。代数余子式是指去掉选定行和列后得到的(n-1)阶子矩阵的行列式,再乘以(-1)^(i+j)(i为选定行的行号,j为选定列的列号)。
下面我们来探讨行列式的基本运算性质,这些性质在行列式的计算和证明中起着至关重要的作用。
性质1:单位矩阵的行列式为1。单位矩阵是指主对角线上的元素都为1,其余元素都为0的矩阵。由于单位矩阵在矩阵乘法中起着类似于数字中的1的作用,因此其行列式为1是合理的。
性质2:行列式与其转置矩阵的行列式相等。转置矩阵是指将矩阵的行和列互换后得到的矩阵。这一性质表明,行列式的计算不依赖于矩阵的行和列的排列顺序,从而简化了行列式的计算过程。
性质3:如果矩阵的某一行(列)是两组数的和,则这个矩阵的行列式等于两个行列式的和,而这两个行列式除了这一行(列)以外全与原行列式相同,但在这一行(列)上,则分别取两组数。这一性质被称为行列式的可加性,它允许我们将复杂的行列式问题分解为更简单的子问题来解决。
性质4:如果矩阵的某一行(列)中的元素都是两数相乘,则这个行列式可以分解为两个行列式的乘积,而这两个行列式除了这一行(列)外都与原行列式相同,但在这一行(列)上,第一个行列式取第一组数的各个元素,而第二个行列式取第二组数的各个对应元素。这一性质被称为行列式的数乘性,它允许我们将行列式问题中的元素进行分解和组合,从而简化计算。
性质5:如果矩阵的某两行(列)互换,则行列式反号。这一性质表明,行列式的计算与矩阵的行(列)的排列顺序有关,但仅当两行(列)互换时,行列式的值才会改变符号。
性质6:如果矩阵的某一行(列)的所有元素都是0,则行列式为0。这一性质是显而易见的,因为任何一行(列)为0的矩阵都可以看作是线性相关的,其行列式必然为0。
性质7:如果矩阵的某两行(列)的元素成比例,则行列式为0。这一性质与性质6类似,也反映了矩阵的线性相关性对行列式的影响。如果两行(列)成比例,那么矩阵的秩将小于其阶数,从而行列式为0。
性质8:行列式的乘法性质:如果A和B都是n阶方阵,则|AB|=|A|×|B|。这一性质表明,行列式在矩阵乘法中具有乘法分配律的性质,它允许我们将复杂的矩阵乘法问题转化为简单的行列式计算问题。
以上性质构成了行列式计算的基础,通过灵活运用这些性质,我们可以简化行列式的计算过程,提高计算效率。
此外,行列式在矩阵理论中还有许多重要的应用。例如,它可以用来判断矩阵是否可逆(即是否存在逆矩阵)。一个n阶方阵A可逆的充分必要条件是其行列式|A|≠0。这是因为,如果|A|=0,则A的秩小于n,即A的列向量线性相关,从而A不存在逆矩阵。反之,如果|A|≠0,则A的列向量线性无关,A存在逆矩阵。
行列式还可以用来求解线性方程组。对于形如Ax=b的线性方程组,如果|A|≠0,则方程组有唯一解x=A^(-1)b(其中A^(-1)表示A的逆矩阵)。这是因为,当|A|≠0时,A的逆矩阵A^(-1)存在,且满足AA^(-1)=I(I为单位矩阵),从而可以通过左乘A^(-1)来求解x。
此外,行列式还与矩阵的特征值、矩阵的秩等概念密切相关。矩阵
- 上一篇: 手机微信无法联网怎么办
- 下一篇: 如何设置CATIA中的凸台
-
 揭秘:代数环的神秘面纱资讯攻略12-07
揭秘:代数环的神秘面纱资讯攻略12-07 -
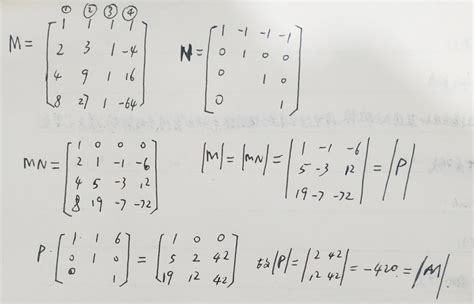 揭秘四阶行列式的计算步骤:轻松掌握高阶行列式求解法资讯攻略10-25
揭秘四阶行列式的计算步骤:轻松掌握高阶行列式求解法资讯攻略10-25 -
 整式运算的高效简便技巧资讯攻略10-29
整式运算的高效简便技巧资讯攻略10-29 -
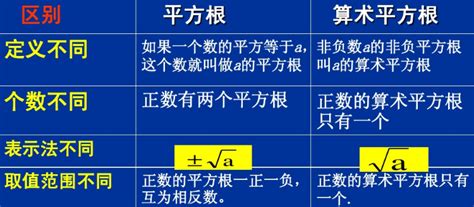 探索平方根公式的奥秘资讯攻略12-03
探索平方根公式的奥秘资讯攻略12-03 -
 cotx的等效公式是什么?资讯攻略12-03
cotx的等效公式是什么?资讯攻略12-03 -
 整式运算的定义与详解资讯攻略10-29
整式运算的定义与详解资讯攻略10-29