三边已知，如何计算三角形面积

在几何学的奇妙世界里，三角形作为最基本的形状之一，承载了无数探索与发现。对于每一个热爱数学、物理乃至艺术的人来说，掌握三角形的各种性质，尤其是如何根据已知的三边长度求解其面积，无疑是一项既实用又充满挑战的技能。今天，就让我们一起揭开这个几何谜题，用轻松有趣的方式，深入探讨“已知三边怎么求三角形面积”的奥秘。

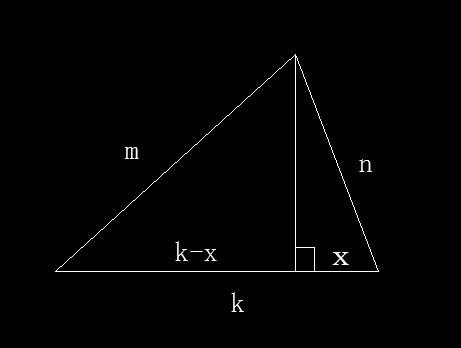
想象一下，你手中拿着一张精美的地图，上面标记了三个点，它们之间用线段相连，形成了一个三角形。这三个点之间的距离（即三角形的三边）已知，但你想知道这个三角形区域到底有多大。这时候，海伦公式就像是一位神秘的向导，引领你穿越几何的迷雾，找到答案。

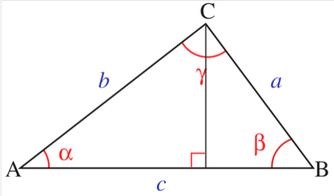
海伦公式，一个听起来就充满古典气息的名词，它最早由古希腊数学家海伦在其著作《测地学》中提出。这个公式神奇之处在于，它仅仅依靠三角形的三边长度，就能精确计算出三角形的面积。具体来说，如果三角形的三边分别为a、b、c，且s为半周长（即s=(a+b+c)/2），那么三角形的面积A就可以通过以下公式求出：

A=√(s(s-a)(s-b)(s-c))

这个公式虽然看起来有些复杂，但实际操作时却异常简洁明了。只需将三角形的三边长度代入公式，经过简单的算术运算，就能得出三角形的面积。是不是觉得既神奇又实用呢？

当然，海伦公式并不是唯一的方法。对于喜欢挑战自我、探索不同解题思路的朋友来说，还有其他几种方法可以求解三角形的面积。比如，利用余弦定理先求出三角形的一个内角，然后再结合三角形的面积公式S=1/2ab*sinC（其中a、b为两边长度，C为这两边所夹的角）进行计算。这种方法虽然相对繁琐一些，但它却为我们提供了一个从不同角度审视三角形面积问题的机会，有助于加深我们对三角形性质的理解。

除了上述方法外，还有一种更为直观、几何化的求解方式——作高法。这种方法通过构造三角形的高线（即从三角形的一个顶点垂直于对边或对边的延长线），将三角形分割成一个或多个易于计算的形状（如矩形、直角三角形等），从而求出三角形的面积。虽然这种方法在已知三边长度的情况下操作起来可能较为复杂（因为需要先通过其他方法求出高的长度），但它却为我们提供了一种直观感受三角形面积的方式，有助于我们更好地把握三角形的几何特征。

在深入探讨了多种求解三角形面积的方法后，我们不禁要问：为什么这些方法能够奏效？它们背后隐藏着怎样的数学原理？其实，这一切都可以追溯到三角形的基本性质上。无论是海伦公式、余弦定理还是作高法，它们都是基于三角形的边长、角度、面积等基本量之间的关系进行推导的。这些关系不仅构成了几何学的基础，也为我们解决实际问题提供了有力的工具。

此外，掌握这些求解三角形面积的方法，不仅有助于我们在数学考试中取得好成绩，更能在我们的日常生活中发挥重要作用。比如，在建筑设计中，我们需要根据房屋的形状和尺寸来计算其面积；在地理测量中，我们需要根据地图上标注的距离来确定某个区域的面积；在艺术创作中，我们需要根据作品的形状和比例来安排画面的布局……这些看似平凡的场景，实则蕴含着深厚的数学原理。而掌握这些原理，无疑会让我们在面对这些问题时更加游刃有余。

值得一提的是，随着科技的进步和计算机技术的发展，现在我们已经可以使用各种软件工具来快速求解三角形的面积。这些工具不仅操作简便、计算准确，还能为我们提供更多的几何信息和可视化效果。然而，无论技术如何发展，掌握基本的数学原理和求解方法始终是我们不可或缺的能力。因为只有这样，我们才能真正理解这些工具背后的原理，才能更好地运用它们来解决实际问题。

最后，让我们回到最初的问题：“已知三边怎么求三角形面积？”通过今天的探讨，相信你已经找到了多种解答这个问题的方法。无论你选择哪种方法，都请记住：数学是一门充满魅力和挑战的学科。它不仅仅是一堆公式和定理的堆砌，更是我们认识世界、改造世界的强大工具。因此，让我们继续在数学的世界里探索前行吧！去发现更多的奥秘、创造更多的奇迹！