根据三角形三边长求面积的方法
在几何学中,三角形是一个基本的形状,其面积的计算对于许多实际问题都至关重要。当我们知道三角形的三边长时,如何求其面积呢?这是一个既经典又实用的问题。下面,我们就来详细探讨一下这个问题,尽量用通俗易懂的语言来解释整个过程。
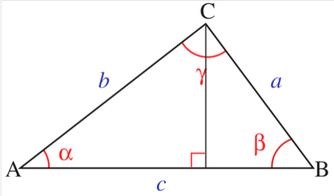
首先,我们需要了解一个叫做“海伦公式”的东西。海伦公式,也叫赫伦公式,是古希腊数学家海伦在《测地术》一书中给出的求三角形面积的一个公式。它告诉我们,如果知道三角形的三边长分别为a、b、c,那么三角形的面积S可以通过下面的公式来计算:
S = √(p(p-a)(p-b)(p-c))
这里的p是三角形的半周长,也就是三边长之和的一半,即p = (a + b + c) / 2。
为什么海伦公式有效?
海伦公式虽然看起来有些复杂,但它实际上是基于一些基本的几何原理和代数运算推导出来的。具体推导过程可能涉及到一些高级的数学知识,比如代数方程和几何证明,但在这里我们可以先不纠结这些,而是直观地理解一下这个公式的合理性。
想象一下,我们有一个三角形,它的三边长是固定的。如果我们尝试改变这个三角形的形状(当然,保持三边长不变),我们会发现这个三角形只能在一个特定的形状下存在,也就是说,它的面积是唯一的。海伦公式正是基于这个唯一性,通过一些巧妙的数学变换,得出了面积的计算公式。
如何使用海伦公式?
使用海伦公式求三角形面积的具体步骤如下:
1. 确定三边长:首先,我们需要知道三角形的三边长a、b、c。这是计算面积的基础。
2. 计算半周长:接着,我们计算三角形的半周长p,即p = (a + b + c) / 2。这一步是为了后续计算方便。
3. 代入公式计算:然后,我们将a、b、c和p代入海伦公式S = √(p(p-a)(p-b)(p-c))中,进行计算。这一步可能需要用到计算器或电脑,因为涉及到开方运算。
4. 得出结果:最后,我们得出三角形的面积S。这个结果是一个数值,表示三角形面积的大小。
举例说明
为了更好地理解海伦公式的使用,我们来举一个具体的例子。
假设我们有一个三角形,它的三边长分别为a = 5,b = 6,c = 7。现在我们要求这个三角形的面积。
1. 确定三边长:a = 5,b = 6,c = 7。
2. 计算半周长:p = (a + b + c) / 2 = (5 + 6 + 7) / 2 = 9。
3. 代入公式计算:S = √(p(p-a)(p-b)(p-c)) = √(9 * (9-5) * (9-6) * (9-7)) = √(9 * 4 * 3 * 2) = √(216) ≈ 14.696(保留四位小数)。
4. 得出结果:所以,这个三角形的面积约为14.696平方单位。
注意事项
在使用海伦公式求三角形面积时,有几点需要注意:
确保三边长满足三角形的条件:即任意两边之和大于第三边。如果三边长不满足这个条件,那么它们不能构成一个三角形,也就无法计算面积。
计算结果的有效性:由于海伦公式涉及到开方运算,因此计算结果可能是一个近似值。在实际应用中,我们可以根据需要保留适当的小数位数。
公式的适用范围:海伦公式只适用于已知三角形三边长求面积的情况。如果已知其他条件(如底和高、两边夹角等),则需要使用其他公式或方法。
其他求三角形面积的方法
除了海伦公式外,还有其他一些方法可以求三角形的面积。这里简要介绍两种常见的方法:
1. 底和高法:如果已知三角形的底和高,那么可以直接使用面积公式S = (底 * 高) / 2来计算。这种方法适用于直角三角形、等腰三角形等特殊情况,也适用于一些可以通过作高转化为特殊三角形的情况。
2. 两边夹角法:如果已知三角形的两边长a、b和它们之间的夹角θ(单位为弧度),那么可以使用面积公式S = (1/2)ab * sinθ来计算。这种方法适用于任意三角形,但需要知道夹角的大小。
实际应用
海伦公式在实际生活中有着广泛的应用。比如,在建筑设计中,我们可能需要计算某个三角形区域的面积来规划空间;在地理信息系统(GIS)中,我们可能需要计算地球表面上某个三角形区域的面积来进行地理分析;在物理学中,我们可能需要计算某个三角形形状的物体的面积来进行力学
- 上一篇: 抖音的访客记录在哪里查看?
- 下一篇: 揭秘!Excel中“.xls”与“.xlsx”后缀的惊人差异
-
 揭秘:用三角形三边长轻松求解面积的秘密方法资讯攻略11-25
揭秘:用三角形三边长轻松求解面积的秘密方法资讯攻略11-25 -
 三角形三边长度求面积方法资讯攻略12-09
三角形三边长度求面积方法资讯攻略12-09 -
 三边已知,如何计算三角形面积资讯攻略11-13
三边已知,如何计算三角形面积资讯攻略11-13 -
 余弦定理有哪些证明方法?资讯攻略10-31
余弦定理有哪些证明方法?资讯攻略10-31 -
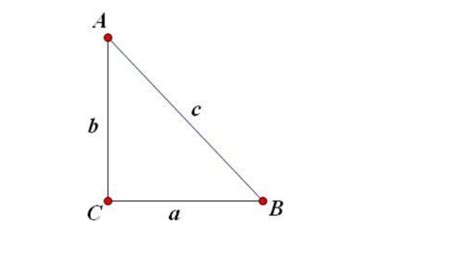 等腰三角形边长计算全攻略资讯攻略10-28
等腰三角形边长计算全攻略资讯攻略10-28 -
 等腰三角形已知底和高,如何求解其边长?资讯攻略10-28
等腰三角形已知底和高,如何求解其边长?资讯攻略10-28