三角形三边长度求面积方法

在数学中，求解三角形的面积是一个基本而重要的技能。当我们知道一个三角形的三边长时，可以通过海伦公式来求解其面积。本文将详细介绍海伦公式及其应用，并通过具体实例和步骤说明如何在已知三角形三边的情况下求出其面积。

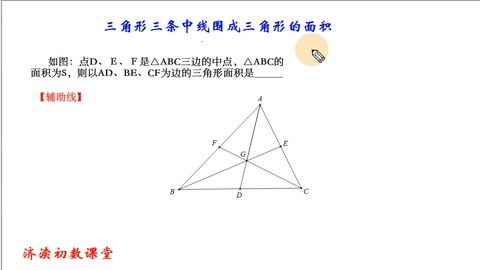
首先，让我们了解一下三角形面积的一些基本概念。三角形的面积通常表示为一个二维空间内由三条边围成的区域的大小。有几种方法可以计算三角形的面积，比如使用底和高、使用向量等。但在只知道三边长的情况下，最常用的方法是海伦公式。

海伦公式，也被称为赫伦公式，是由古希腊数学家海伦在其著作《测地学》中提出的。该公式允许我们在仅知道三角形三边长度的情况下计算其面积。海伦公式的基本形式如下：

设三角形的三边长分别为a、b和c，半周长p为三边长之和的一半，即p = (a + b + c) / 2。那么三角形的面积S可以通过以下公式计算：

S = √[p(p - a)(p - b)(p - c)]

这个公式看起来有些复杂，但我们可以分步骤来理解和应用它。

步骤一：计算半周长p

首先，我们需要计算三角形的半周长p。这是通过将三角形的三边长a、b和c相加，然后除以2来得到的。

例如，对于一个三边长分别为5、6和7的三角形，我们可以这样计算半周长p：

p = (5 + 6 + 7) / 2 = 9

步骤二：将p代入海伦公式

接下来，我们将计算得到的半周长p代入海伦公式中。海伦公式为：

S = √[p(p - a)(p - b)(p - c)]

将p、a、b和c的值代入公式，进行计算。

继续以三边长分别为5、6和7的三角形为例，我们可以这样计算面积S：

S = √[9 × (9 - 5) × (9 - 6) × (9 - 7)]

= √[9 × 4 × 3 × 2]

= √[216]

≈ 14.7（四舍五入到小数点后一位）

因此，这个三角形的面积约为14.7平方单位。

验证和注意事项

在使用海伦公式计算三角形面积时，有一些重要的注意事项需要牢记：

1. 三边关系：三边长必须满足三角形的两边之和大于第三边的条件，即a + b > c，a + c > b，b + c > a。如果不满足这些条件，那么给定的边长不能构成一个三角形。

2. 数值精度：在计算过程中，特别是当边长是近似值时，要注意数值的精度。由于计算过程中涉及平方和开方运算，微小的误差可能会导致结果有较大的偏差。

3. 符号约定：在数学中，三角形的面积通常表示为正值。但在某些情况下，例如在解析几何或向量几何中，可能会遇到负值的情况，这通常表示方向或定向面积。在使用海伦公式时，我们不需要考虑方向，因为公式本身只给出面积的绝对值。

此外，海伦公式不仅可以用于计算普通三角形的面积，还可以用于计算一些特殊类型的三角形的面积，如等腰三角形、等边三角形和直角三角形。对于等腰三角形和等边三角形，由于存在对称性或边长相等的特点，可以使用更简单的公式来计算面积。然而，这些简化公式在本质上是海伦公式的特例。

应用实例

海伦公式在几何学和工程学中有广泛的应用。以下是一些具体的例子：

地理学：在地图上测量和计算不同地点之间的距离和面积时，海伦公式可以用于计算由这些地点构成的三角形的面积。

建筑学：在建筑设计中，设计师可能需要计算房间或空间的面积。如果房间的形状是三角形，那么海伦公式就非常有用。

工程学：在土木工程和机械工程中，经常需要计算由梁、柱等结构件构成的三角形的面积。这些面积可以用于计算应力、应变和材料用量等。

实际应用中的步骤

在实际应用中，使用海伦公式计算三角形面积的步骤通常包括以下几个阶段：

1. 收集数据：首先，需要收集三角形的三边长数据。这些数据可以通过测量、计算或查阅相关文件得到。

2. 计算半周长：将收集到的三边长数据相加，然后除以2，得到半周长p。

3. 代入公式计算：将计算得到的半周长p和原始的三边长a、b和c代入海伦公式，进行计算。

4. 解释结果：最后，根据计算结果解释三角形的面积。这可能涉及将面积单位转换为更合适的单位，或根据需要进行四舍五入等。

结论

海伦公式是一个强大而简单的工具，它允许我们在仅知道三角形三边长的情况下计算其面积。通过遵循上述步骤和注意事项，我们可以准确地计算任何