揭秘圆的面积计算方法:轻松掌握几何奥秘
在这个充满奇妙图形的世界里,圆形无疑是最具魅力和普遍性的几何形状之一。无论是自然界中的太阳、月亮,还是人造物品如车轮、盘子,圆都以其独特的形态和完美的对称性吸引着我们的目光。但你是否曾好奇,这个看似简单的形状,其面积究竟是如何计算的呢?今天,就让我们一起揭开圆面积计算的神秘面纱,探索那些隐藏在圆中的数学奥秘。

首先,我们要明白什么是圆。圆是平面上所有与给定点(称为圆心)距离相等的点的集合。这个给定的距离,我们通常称之为半径。圆心和半径是定义圆的基本要素,也是后续计算圆面积不可或缺的参数。

当我们谈论圆的面积时,实际上是在讨论这个圆形区域所占的平面空间大小。想象一下,你手里有一个圆形的纸片,你希望知道这个纸片覆盖了多大的面积。这时候,我们就需要用到一个专门的公式来计算它。

那么,这个神奇的公式是什么呢?它就是:圆的面积 = π × 半径^2。
看到这里的你,可能会对这个公式中的“π”(Pi,圆周率)感到陌生。但别担心,π是数学中一个非常重要的常数,它约等于3.14159,是一个无理数,即它的小数部分是无限不循环的。尽管我们无法准确地说出π的完整数值,但它在计算圆的面积、周长等属性时却起着至关重要的作用。
现在,让我们来详细解析一下这个公式。首先,“半径^2”表示半径的平方,即将半径乘以自己。这个操作是为了确保面积的计算与半径的长度成平方关系。换句话说,如果圆的半径增加一倍,其面积将增加四倍(因为半径的平方增加了四倍)。
而π则是一个比例因子,它确保了计算结果的准确性。没有π,我们就无法精确地描述圆的面积与半径之间的关系。因此,π的存在是圆面积计算中不可或缺的一部分。
接下来,让我们通过一些具体的例子来加深对这个公式的理解。
假设你有一个半径为3厘米的圆形纸片。想要知道它的面积,你只需要将半径(3厘米)代入公式中,并进行计算:面积 = π × 3^2 = π × 9 ≈ 3.14 × 9 = 28.26平方厘米。
再举一个例子,如果你有一个半径为5米的圆形花坛,想要知道它的面积有多大,同样可以使用这个公式:面积 = π × 5^2 = π × 25 ≈ 3.14 × 25 = 78.5平方米。
通过这些例子,我们可以看到,使用圆面积公式进行计算是非常简单且直观的。只需要知道圆的半径,就可以轻松地求出其面积。
当然,在实际生活中,我们可能会遇到一些更加复杂的情况。比如,你可能需要计算一个椭圆形或扇形的面积。虽然这些形状与圆形有所不同,但它们的面积计算仍然与圆有着密切的联系。
对于椭圆形来说,其面积可以通过长轴和短轴的乘积再乘以π来近似计算(但需要注意的是,这个公式是椭圆面积的近似值,不是精确值)。而对于扇形来说,其面积则可以通过圆的面积乘以扇形的圆心角与360度的比值来计算。
此外,圆面积的计算在日常生活和工程实践中也有着广泛的应用。比如,在建筑设计中,我们可能需要计算圆形房间的面积来确定家具的摆放和布局;在机械制造中,我们可能需要计算圆形零件的面积来估算材料的使用量;在农业生产中,我们可能需要计算圆形农田的面积来规划作物的种植和灌溉等。
总之,圆面积的计算不仅是一个简单的数学问题,更是一个与我们的生活息息相关的实用技能。掌握了这个技能,我们就能够更好地理解和利用圆形这个美妙的几何形状,为我们的生活和工作带来更多的便利和乐趣。
在结束这篇文章之前,我想再提醒大家一点:虽然π是一个无理数,无法准确表示为一个有限小数或分数,但在实际计算中,我们通常会使用其近似值(如3.14或更精确的数值)来进行计算。这样做既方便又实用,能够满足我们大多数情况下的需求。当然,在某些对精度要求极高的场合下,我们需要使用更精确的π值来进行计算,以确保结果的准确性。
现在,你已经了解了圆面积的计算方法和其在生活中的应用。下次当你看到圆形物体时,不妨试着用你学到的知识来计算一下它的面积吧!相信通过实践,你会对这个公式有更深刻的理解和掌握。
- 上一篇: 掌握HD Tune Pro:高效硬盘检测与优化指南
- 下一篇: 《黑手党:黑帮之城 游戏攻略指南》
-
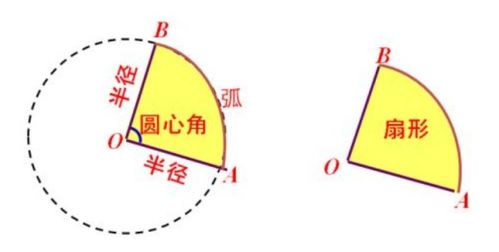 扇形面积计算的三大公式是什么?资讯攻略10-25
扇形面积计算的三大公式是什么?资讯攻略10-25 -
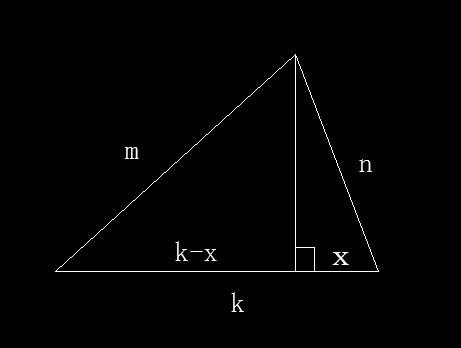 三边已知,如何计算三角形面积资讯攻略11-13
三边已知,如何计算三角形面积资讯攻略11-13 -
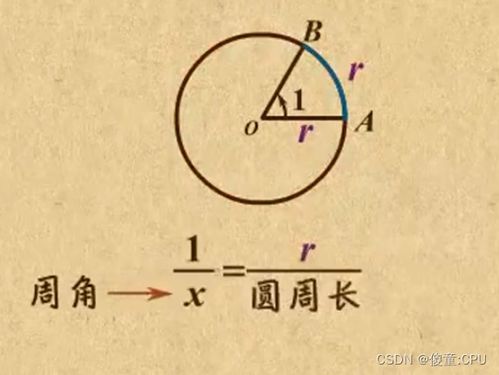 探索弧度的奥秘:轻松学会计算方法资讯攻略11-06
探索弧度的奥秘:轻松学会计算方法资讯攻略11-06 -
 揭秘等腰三角形边长计算的奥秘公式资讯攻略11-16
揭秘等腰三角形边长计算的奥秘公式资讯攻略11-16 -
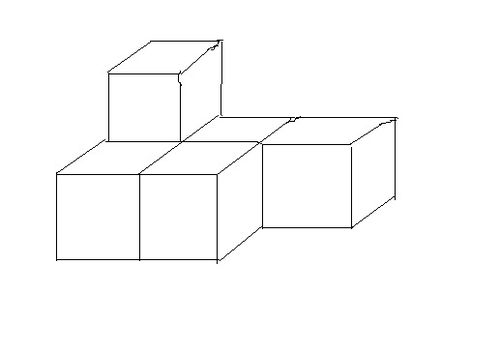 揭秘正方体体积的求解奥秘资讯攻略11-16
揭秘正方体体积的求解奥秘资讯攻略11-16 -
 一亩三分地,究竟长宽几何?揭秘其尺寸!资讯攻略12-05
一亩三分地,究竟长宽几何?揭秘其尺寸!资讯攻略12-05












