计算机中-1的补码表示是什么
在计算机科学的广阔天地里,数据表示与处理是至关重要的一环。当我们谈论数字时,无论是正数还是负数,在计算机内部都有其特定的表示方式。今天,我们就来深入探讨一个看似简单却内涵丰富的主题:计算机中-1的补码是什么。希望通过这篇通俗易懂的文章,你能对这个概念有更全面的理解。

首先,要明白计算机是如何存储和处理数据的,我们得先了解二进制。在计算机的世界里,所有的信息,无论是文字、图像还是声音,最终都被转化为二进制代码,也就是0和1的组合。对于整数,计算机通常采用固定位数的二进制来表示,比如8位、16位、32位或64位。在这里,我们以8位二进制为例来解释。

原码、反码与补码
在计算机中,一个数可以有三种不同的二进制表示方式:原码、反码和补码。这三种编码方式在处理正数和负数时有所不同。

1. 原码:
原码是最直观的表示方式。对于正数,原码就是其二进制形式,符号位为0。对于负数,原码则是符号位为1,其余位表示该数的绝对值。
例如,8位二进制下,+1的原码是00000001,-1的原码是10000001。
2. 反码:
正数的反码与原码相同。
负数的反码是在原码的基础上,符号位不变,其余位取反。
例如,+1的反码是00000001,-1的反码是11111110。
3. 补码:
正数的补码与原码、反码都相同。
负数的补码是在反码的基础上加1。
例如,+1的补码是00000001,-1的补码是11111111。
为什么需要补码
在计算机发展的早期,原码和反码都曾被用来表示负数,但它们都存在一些问题。原码最直接的问题是无法直接进行减法运算,因为符号位参与运算会导致结果不正确。反码虽然解决了原码做减法时符号位的问题,但在表示0时却出现了+0和-0两个编码,这不仅增加了复杂性,而且在实际应用中并没有意义。
补码的出现解决了这些问题。首先,补码允许符号位参与运算,从而可以直接用加法来实现减法(减去一个数等于加上这个数的负数)。其次,补码表示法中,0只有一个编码(即全0),避免了+0和-0的混淆。最重要的是,补码还能多表示一个数(在8位二进制中,补码能表示的范围是-128到127,而原码和反码只能表示-127到127)。
1的补码详解
现在,我们回到文章的主题:计算机中-1的补码是什么?
1. 确定位数:
首先,我们需要明确是使用多少位的二进制来表示这个数。在这里,我们以8位二进制为例。
2. 计算原码:
对于-1,其8位二进制的原码是10000001。这里,最高位是符号位,1表示负数;其余位表示-1的绝对值(即1)的二进制形式(但因为是负数,所以这里实际上表示的是-1的补码形式中的绝对值部分,但在原码表示中直接这样写)。
3. 计算反码:
在原码的基础上,将符号位以外的所有位取反,得到-1的8位二进制反码是11111110。
4. 计算补码:
在反码的基础上加1,得到-1的8位二进制补码是11111111。
所以,计算机中-1的8位二进制补码就是11111111。
补码的应用与意义
补码不仅简化了计算机的运算过程(如允许用加法代替减法),而且提高了数据表示的效率和准确性(如避免了+0和-0的混淆,以及能多表示一个数)。在现代计算机中,无论是CPU内部的寄存器、内存中的数据,还是硬盘上的存储文件,都广泛采用补码来表示整数。
补码的应用不仅限于整数表示。在浮点数表示中,虽然IEEE 754标准采用的是一种更复杂的编码方式(包括符号位、指数位和尾数位),但补码的概念仍然在其中发挥着重要作用(特别是在表示指数和尾数的符号时)。此外,在计算机网络、数据库系统、图像处理等领域,补码也都有着广泛的应用。
结语
通过这篇文章的介绍,相信你已经对计算机中-1的补码有了更深入的理解。补码不仅是计算机内部数据表示的一种重要方式,更是计算机能够进行高效、准确运算的基础。从原码到反码再到补码的发展过程,不仅体现了人类对计算机科学的不断探索和创新,也为我们今天能够享受到的便捷、高效的数字生活奠定了坚实的基础。希望这篇文章能够激发你对计算机科学更浓厚的兴趣,让你在未来的学习和探索中收获更多知识和乐趣。
-
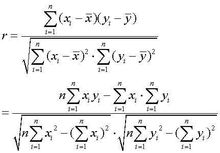 揭秘:相关系数计算全攻略资讯攻略11-03
揭秘:相关系数计算全攻略资讯攻略11-03 -
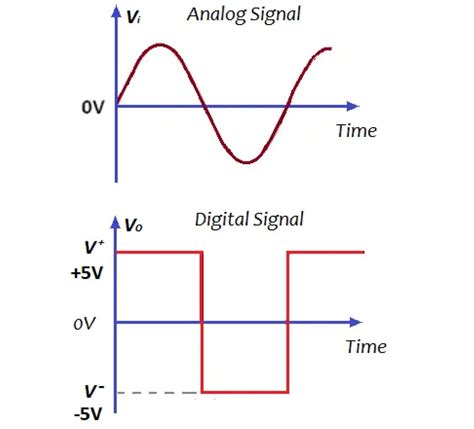 揭秘:数字信号究竟是什么?资讯攻略01-14
揭秘:数字信号究竟是什么?资讯攻略01-14 -
 阶乘的定义与公式资讯攻略03-25
阶乘的定义与公式资讯攻略03-25 -
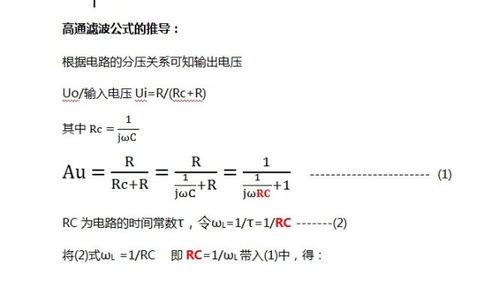 频率的计算公式是什么资讯攻略11-13
频率的计算公式是什么资讯攻略11-13 -
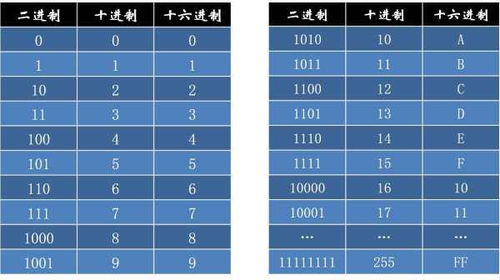 揭秘:十六进制中的神秘字母代表什么?资讯攻略11-02
揭秘:十六进制中的神秘字母代表什么?资讯攻略11-02 -
 如何计算百分位数?资讯攻略11-29
如何计算百分位数?资讯攻略11-29