转速与角速度:轻松掌握转换公式
转速和角速度的转换公式详解
在机械工程和物理学中,转速和角速度是描述旋转运动的重要参数。虽然它们都用来描述旋转的快慢,但物理意义和度量单位却有所不同。转速通常表示为每分钟转过的圈数(RPM,Revolution Per Minute),而角速度则是以弧度每秒(rad/s)为单位。为了更好地理解和应用这两个概念,我们需要了解它们之间的转换公式。

一、转速和角速度的基本概念

转速,即旋转速度,是描述物体在单位时间内旋转的次数或圈数。常见的单位是每分钟转数(RPM),即每分钟内物体旋转的完整圈数。转速是直观且易于理解的,例如汽车发动机的转速表显示的就是发动机的转速。
角速度,则是描述物体在单位时间内绕某一轴旋转的角度。角速度的单位通常是弧度每秒(rad/s),其中弧度是角度的一种度量方式,与度(°)不同,但可以通过一定的换算关系相互转换。一个完整的圆周长对应的角度是2π弧度,因此一圈(360°)等于2π弧度。
二、转速和角速度的关系
转速和角速度之间的关系可以通过以下公式进行转换:
角速度(ω)= 转速(n)× 2π / 60
或者简化为:
ω = n × π / 30
这个公式表明,角速度是转速与2π除以60的乘积,即每分钟转速乘以π再除以30。这是因为每分钟有60秒,而一圈(360°)等于2π弧度,所以要将转速从每分钟转数转换为每秒转过的弧度数,就需要乘以2π再除以60。
反之,如果我们知道角速度,也可以通过以下公式求解转速:
转速(n)= 角速度(ω)× 30 / π
或者简化为:
n = ω × 60 / (2π)
这个公式表示,转速是角速度与30除以π的乘积,即每秒转过的弧度数乘以30再除以π,或者每秒转过的弧度数乘以60再除以2π(因为每分钟有60秒)。
三、转速和角速度转换公式的应用
1. 机械工程领域
在机械工程领域,转速和角速度的转换公式广泛应用于各种旋转机械的设计和分析中。例如,在设计汽车发动机时,需要了解发动机的转速与曲轴角速度之间的关系,以确保发动机的正常运行和性能优化。同样,在制造风力发电机时,也需要根据转速和角速度的关系来确定发电机的最佳转速和输出功率。
2. 物理学研究
在物理学研究中,转速和角速度的转换公式对于理解旋转物体的运动规律和力学性质具有重要意义。例如,在研究刚体的转动惯量和角动量时,需要了解转速和角速度之间的转换关系,以便进行准确的计算和分析。此外,在研究旋转物体的动力学问题时,如陀螺仪的稳定性和自旋稳定等,也需要利用转速和角速度的转换公式来求解相关参数。
3. 航空航天领域
在航空航天领域,转速和角速度的转换公式对于确保飞行器的稳定性和安全性至关重要。例如,在导弹和火箭的制导系统中,需要精确测量和控制飞行器的转速和角速度,以确保其按照预定的轨迹和姿态进行飞行。此外,在卫星的姿态控制系统中,也需要利用转速和角速度的转换公式来实时调整卫星的姿态和轨道。
4. 日常生活中的应用
除了专业领域的应用外,转速和角速度的转换公式在日常生活中也有广泛的应用。例如,在使用电动工具(如电钻、砂轮机等)时,我们需要了解工具的转速和角速度,以便选择合适的转速和工具类型来完成工作任务。同样,在骑自行车或摩托车时,我们也需要了解车轮的转速和角速度,以判断车辆的行驶速度和稳定性。
四、实例分析
为了更好地理解转速和角速度的转换公式,我们可以通过一个具体的实例进行分析。假设有一个汽车发动机的转速为6000RPM,我们需要计算其对应的角速度。
根据转速和角速度的转换公式:
ω = n × π / 30
将n=6000代入公式中,得到:
ω = 6000 × π / 30 = 200π rad/s
因此,该汽车发动机的角速度为200π弧度每秒。
反之,如果我们知道一个旋转物体的角速度为100π rad/s,我们需要计算其对应的转速。
根据转速和角速度的转换公式:
n = ω × 30 / π
将ω=100π代入公式中,得到:
n = 100π × 30 / π = 3000 RPM
因此,该旋转物体的转速为3000RPM。
五、结论
转速和角速度是
- 上一篇: 轻松学!月饼简笔画的绘制秘籍
- 下一篇: 2023年护师考试成绩快速查询指南
-
 转速与角速度转换公式详解资讯攻略11-05
转速与角速度转换公式详解资讯攻略11-05 -
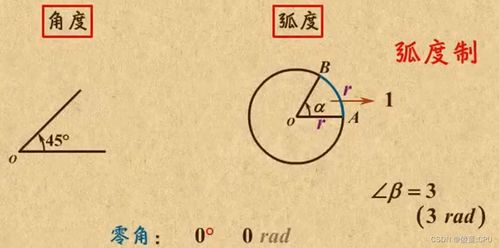 角度与弧度轻松转换秘籍资讯攻略11-25
角度与弧度轻松转换秘籍资讯攻略11-25 -
 如何轻松检测电脑风扇转速的实用方法资讯攻略03-10
如何轻松检测电脑风扇转速的实用方法资讯攻略03-10 -
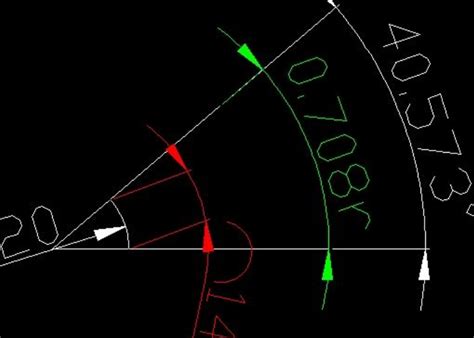 角度制与弧度制相互转换的公式是什么资讯攻略10-29
角度制与弧度制相互转换的公式是什么资讯攻略10-29 -
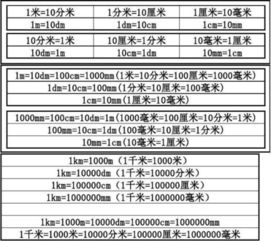 200毫米是多少米?资讯攻略03-01
200毫米是多少米?资讯攻略03-01 -
 是否需要将笔记本硬盘从5400转升级至7200转?资讯攻略11-21
是否需要将笔记本硬盘从5400转升级至7200转?资讯攻略11-21











