角度与弧度轻松转换秘籍
在数学的世界里,角度和弧度是描述旋转或圆周运动的两种基本单位。它们虽然形式不同,但实则紧密相连,通过简单的转换公式就能轻松实现相互转换。无论是学习三角函数、物理运动分析,还是进行工程设计,角度与弧度的转换都是必不可少的技能。下面,我们就来详细探讨一下角度与弧度转换公式的方方面面,让你轻松掌握这一数学工具。
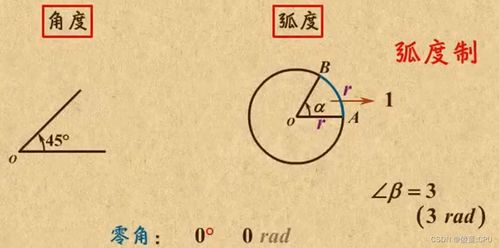
角度:生活中的直观感受
提到角度,我们脑海中可能会浮现出钟表上的指针、扇形的面积,或是建筑物中角度精确的屋顶。角度是用来测量平面角大小的单位,通常用度(°)来表示。一个完整的圆周被等分为360度,这也是我们日常生活中最为熟悉的角度单位。
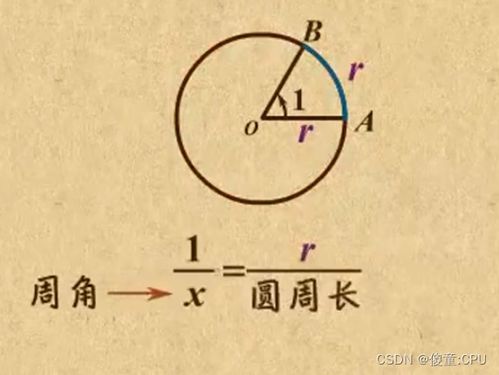
例如,时钟上的时针每过一小时,就会旋转30°(因为360°/12小时=30°/小时)。当我们说一个直角是90°时,意味着这个角是由两条垂直相交的直线形成的。角度的直观性和易理解性,使得它在日常生活和初等教育中得到了广泛应用。
弧度:数学中的优雅表达
与角度不同,弧度(rad)是数学和物理学中更为常用的旋转度量单位。弧度制的引入,使得很多数学公式和定理变得更加简洁和优美。在弧度制下,一个完整的圆周等于2π(约等于6.28)弧度。
为什么选择π作为圆周与弧度的关系呢?这是因为弧度制与圆的半径直接相关。想象一个半径为r的圆,如果圆上的一段弧长等于半径r,那么这段弧所对应的圆心角就是1弧度。因此,一个完整的圆周(弧长等于2πr)对应的圆心角就是2π弧度。
转换公式:架起角度与弧度的桥梁
要实现角度与弧度之间的转换,我们需要记住两个简单的公式:
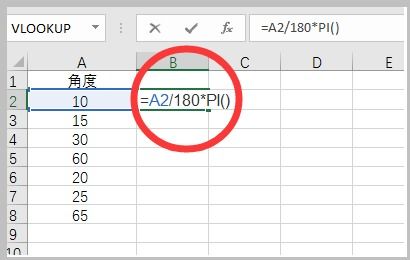
1. 角度转弧度:弧度 = 角度 × (π/180)
2. 弧度转角度:角度 = 弧度 × (180/π)
这两个公式是角度与弧度转换的核心,它们将两种度量单位紧密地联系在了一起。下面,我们通过几个例子来演示这些公式的应用。
例子1:角度转弧度
假设我们有一个45°的角,想要知道它对应的弧度是多少。根据转换公式,我们可以这样计算:
弧度 = 45° × (π/180) = π/4
因此,45°对应的弧度是π/4。
例子2:弧度转角度
现在,我们有一个π/3弧度的角,想要知道它对应的角度是多少。同样地,利用转换公式,我们可以得到:
角度 = π/3 × (180/π) = 60°
所以,π/3弧度对应的角度是60°。
为什么要进行转换?
你可能会好奇,既然角度和弧度都能用来描述旋转,为什么还要进行转换呢?事实上,角度和弧度各有其优势和适用场景。
角度的优势:角度制更直观,易于理解,特别是在日常生活中。比如,我们习惯于说“这个角是45°”,而不是“这个角是π/4弧度”。
弧度的优势:在微积分、三角函数、物理等领域,弧度制更为方便。例如,在计算导数、积分以及解决与圆周运动相关的问题时,使用弧度制可以大大简化计算过程。此外,弧度制还使得三角函数具有一些美丽的性质,如sin(x)的导数仍然是cos(x),这些在角度制下是无法直接观察到的。
实际应用中的转换
在解决实际问题时,角度与弧度的转换常常是无形的,但又是必不可少的。以下是一些具体的应用场景:
三角函数计算:在计算三角函数值时,输入的角度通常以度为单位,但计算器或数学软件内部通常使用弧度制进行计算。因此,在输入之前,我们需要将角度转换为弧度。
物理运动分析:在物理学中,描述圆周运动或摆动时,经常会用到弧度制。比如,计算一个物体在圆周轨道上的线速度或角速度时,就需要用到弧度来表示角度。
工程设计:在机械、电子等工程领域,设计旋转部件或计算齿轮传动比时,也经常需要进行角度与弧度的转换。
总结
角度与弧度是描述旋转运动的两种基本单位,它们各有其优势和适用场景。通过简单的转换公式,我们可以轻松地在两者之间进行转换。掌握这一技能,不仅能够帮助我们更好地理解数学和物理知识,还能在实际应用中提高计算效率和准确性。
在日常生活中,我们可以保持对角度的直观感受;但在进行数学计算或解决物理问题时,不妨尝试一下弧度制,你可能会发现它带来的便利和优雅。无论是角度还是弧度,它们都是数学世界中的宝贵工具,帮助我们更好地认识和探索这个充满奥秘的宇宙。
- 上一篇: 揭秘:计算机硬件的构成部件有哪些?
- 下一篇: 宝宝换奶粉的正确步骤指南
-
 如何将弧度转换为角度?资讯攻略11-09
如何将弧度转换为角度?资讯攻略11-09 -
 Win10计算器中将角度转换为弧度的方法资讯攻略11-09
Win10计算器中将角度转换为弧度的方法资讯攻略11-09 -
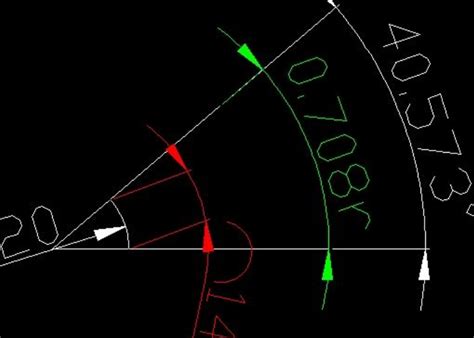 角度制与弧度制相互转换的公式是什么资讯攻略10-29
角度制与弧度制相互转换的公式是什么资讯攻略10-29 -
 角度制和弧度制之间如何转换?资讯攻略11-09
角度制和弧度制之间如何转换?资讯攻略11-09 -
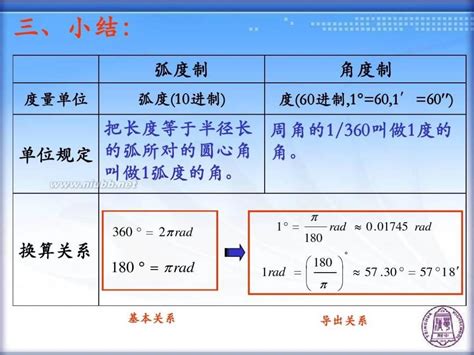 轻松掌握:弧度与角度的换算方法资讯攻略11-15
轻松掌握:弧度与角度的换算方法资讯攻略11-15 -
 揭秘:1度与弧度之间的神秘换算关系资讯攻略01-09
揭秘:1度与弧度之间的神秘换算关系资讯攻略01-09











